Bayes’ Theorem

Mark Lai
January 7, 2022 
library(tidyverse)
theme_set(theme_classic() +
    theme(panel.grid.major.y = element_line(color = "grey92")))

Bayes’s Theorem

The Bayes’s theorem is, surprisingly (or unsurprisingly), very simple:

\[P(B \mid A) = \frac{P(A \mid B) P(B)}{P(A)}\]

More generally, we can expand it to incorporate the law of total probability to make it more applicable to data analysis. Consider \(B_i\) as one of the \(n\) many possible mutually exclusive events, then \[\begin{align} P(B_i \mid A) & = \frac{P(A \mid B_i) P(B_i)}{P(A)} \\ & = \frac{P(A \mid B_i) P(B_i)} {P(A \mid B_1)P(B_1) + P(A \mid B_2)P(B_2) + \cdots + P(A \mid B_n)P(B_n)} \\ & = \frac{P(A \mid B_i) P(B_i)}{\sum_{k = 1}^n P(A \mid B_k)P(B_k)} \end{align}\]

If \(B_i\) is a continuous variable, we will replace the sum by an integral, \[P(B_i \mid A) = \frac{P(A \mid B_i) P(B_i)}{\int_k P(A \mid B_k)P(B_k)}\] The denominator is not important for practical Bayesian analysis, therefore, it is sufficient to write the above equality as

\[P(B_i \mid A) \propto P(A \mid B_i) P(B_i)\]

Example 1: Base rate fallacy (From Wikipedia)

A police officer stops a driver at random and does a breathalyzer test for the driver. The breathalyzer is known to detect true drunkenness 100% of the time, but in 1% of the cases, it gives a false positive when the driver is sober. We also know that in general, for every 1,000 drivers passing through that spot, one is driving drunk. Suppose that the breathalyzer shows positive for the driver. What is the probability that the driver is truly drunk?

\(P(\text{positive} | \text{drunk}) = 1\)
\(P(\text{positive} | \text{sober}) = 0.01\)
\(P(\text{drunk}) = 1 / 1000\)
\(P(\text{sober}) = 999 / 1000\)

Using Bayes’ Theorem,

\[\begin{align} P(\text{drunk} | \text{positive}) & = \frac{P(\text{positive} | \text{drunk}) P(\text{drunk})} {P(\text{positive} | \text{drunk}) P(\text{drunk}) + P(\text{positive} | \text{sober}) P(\text{sober})} \\ & = \frac{1 \times 0.001}{1 \times 0.001 + 0.01 \times 0.999} \\ & = 100 / 1099 \approx 0.091 \end{align}\]

So there is less than a 10% chance that the driver is drunk even when the breathalyzer shows positive.

You can verify that with a simulation using R:

set.seed(4)
truly_drunk <- c(rep("drunk", 100), rep("sober", 100 * 999))
table(truly_drunk)

#> truly_drunk
#> drunk sober 
#>   100 99900
breathalyzer_test <- ifelse(truly_drunk == "drunk",
    # If drunk, 100% chance of showing positive
    "positive",
    # If not drunk, 1% chance of showing positive
    sample(c("positive", "negative"), 999000,
        replace = TRUE, prob = c(.01, .99)
    )
)
# Check the probability p(positive | sober)
table(breathalyzer_test[truly_drunk == "sober"])

#> 
#> negative positive 
#>    98903      997
# 997 / 99900 = 0.00997998, so the error rate is less than 1%
# Now, Check the probability p(drunk | positive)
table(truly_drunk[breathalyzer_test == "positive"])

#> 
#> drunk sober 
#>   100   997
# 100 / (100 + 997) = 0.0911577, which is only 9.1%!

Bayesian Statistics

Bayesian statistics is a way to estimate some parameter \(\theta\) (i.e., some quantities of interest, such as the population mean, regression coefficient, etc) by applying the Bayes’ Theorem. > \[P(\theta | D) \propto P(D | \theta) P(\theta)\]

There are three components in the above equality:

On the other hand, classical/frequentist statistics focuses solely on the likelihood function.1 In Bayesian statistics, the goal is to update one’s belief about \(\theta\) based on the observed data \(D\).

Example 2: Locating a Plane

Consider a highly simplified scenario of locating a missing plane in the sea. Assume that we know the plane, before missing, happened to be flying on the same latitude, heading west across the Pacific, so we only need to find the longitude of it. We want to go out to collect debris (data) so that we can narrow the location (\(\theta\)) of the plane down.

We start with our prior. Assume that we have some rough idea that the plane should be, so we express our belief in a probability distribution like the following:

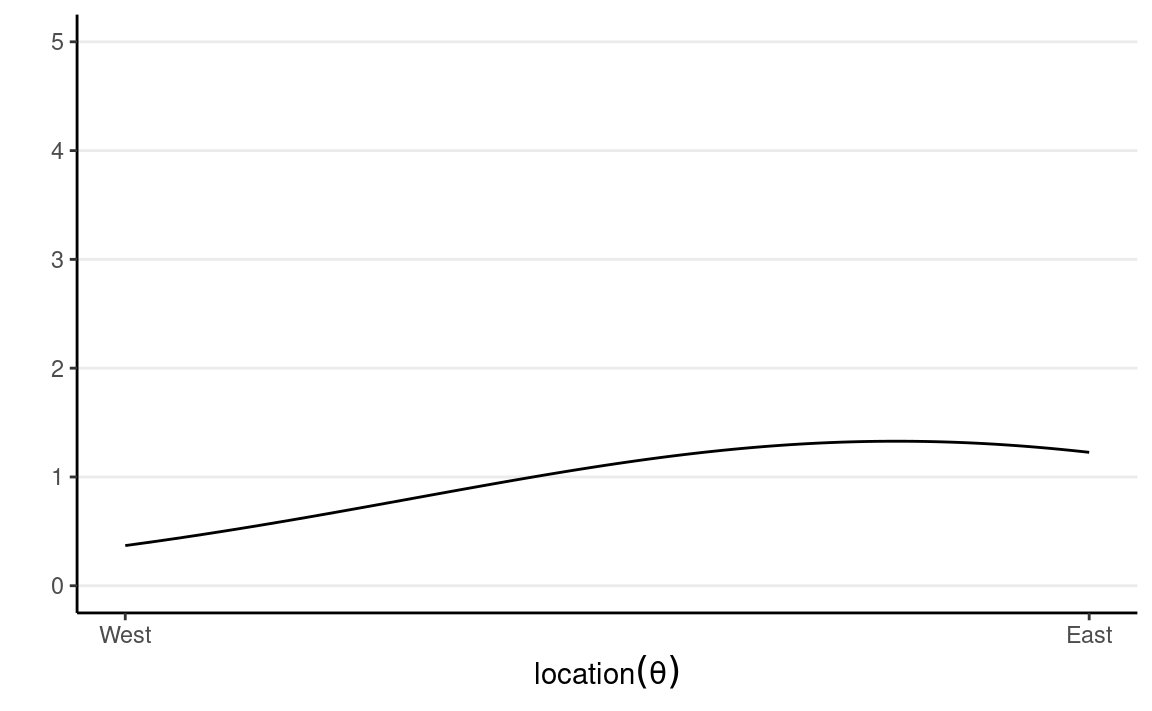
which says that our belief is that the plane is about twice more likely to be towards the east than towards the west. Below are two other options for priors (out of infinitely many), one providing virtually no information and the other encoding stronger information:

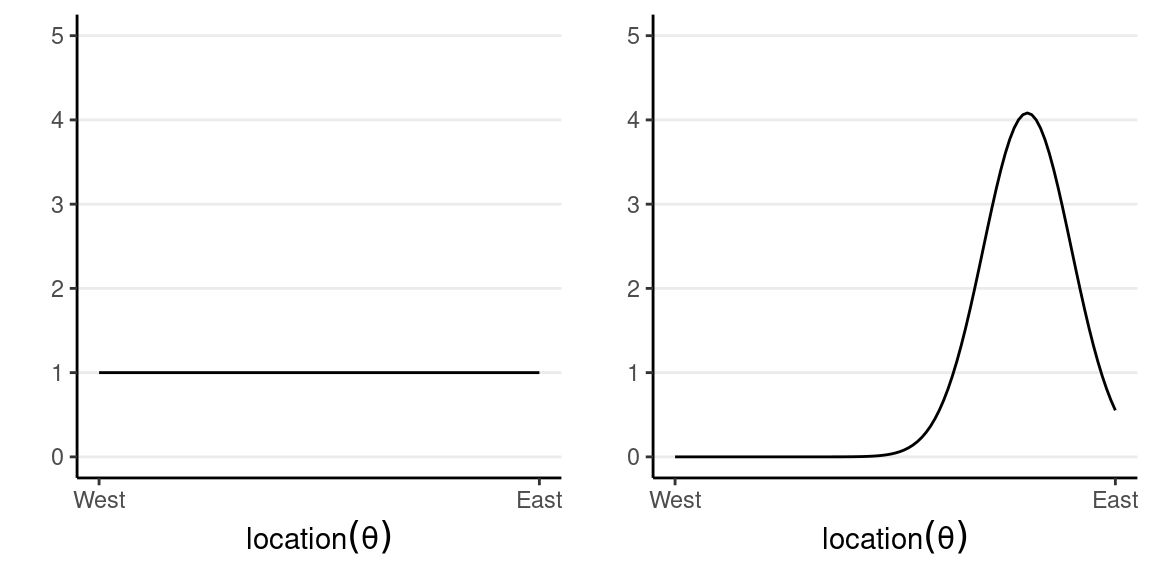
The prior is chosen to reflect the researcher’s belief, so it is likely that different researchers will formulate a different prior for the same problem, and that’s okay as long as the prior is reasonable and justified. Later we will learn that in regular Bayesian analyses, with moderate sample size, different priors generally make only negligible differences.

Now, assume that we have collected debris in the locations shown in the graph,

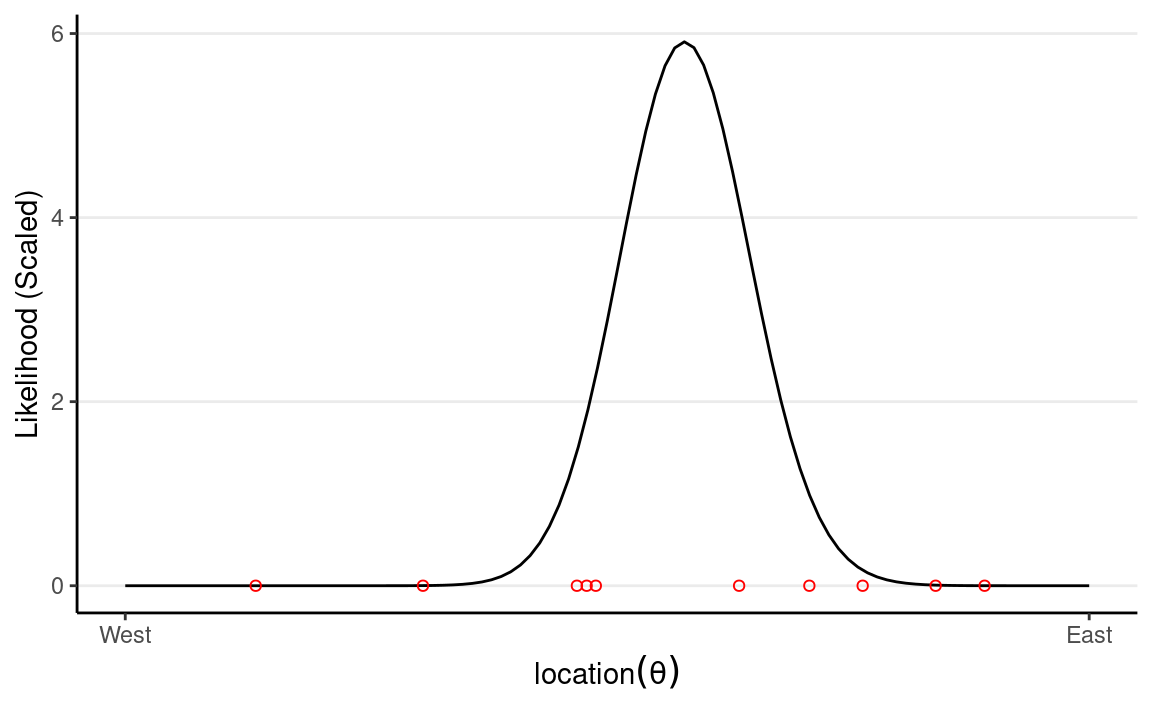
Now, from Bayes’s Theorem,

\[\text{Posterior Probability} \propto \text{Prior Probability} \times \text{Likelihood}\]

So we can simply multiply the prior probabilities and the likelihood to get the posterior probability for every location. A rescaling step is needed to ensure that the area under the curve will be 1, which is usually performed by the software.

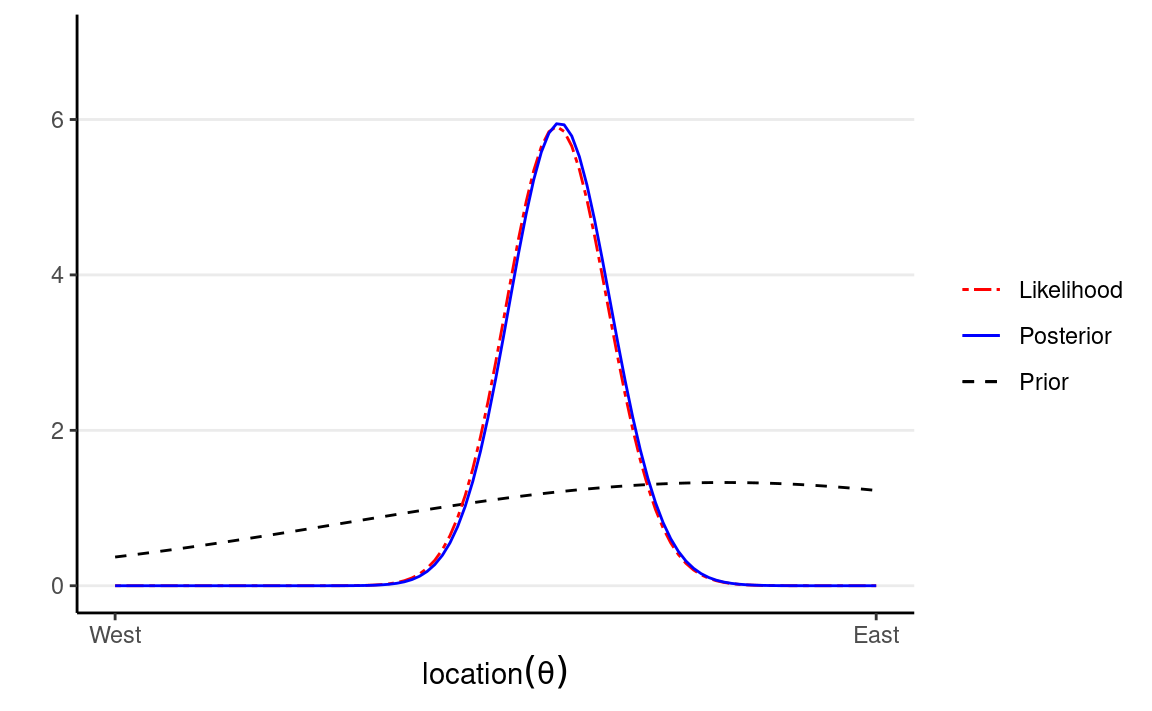
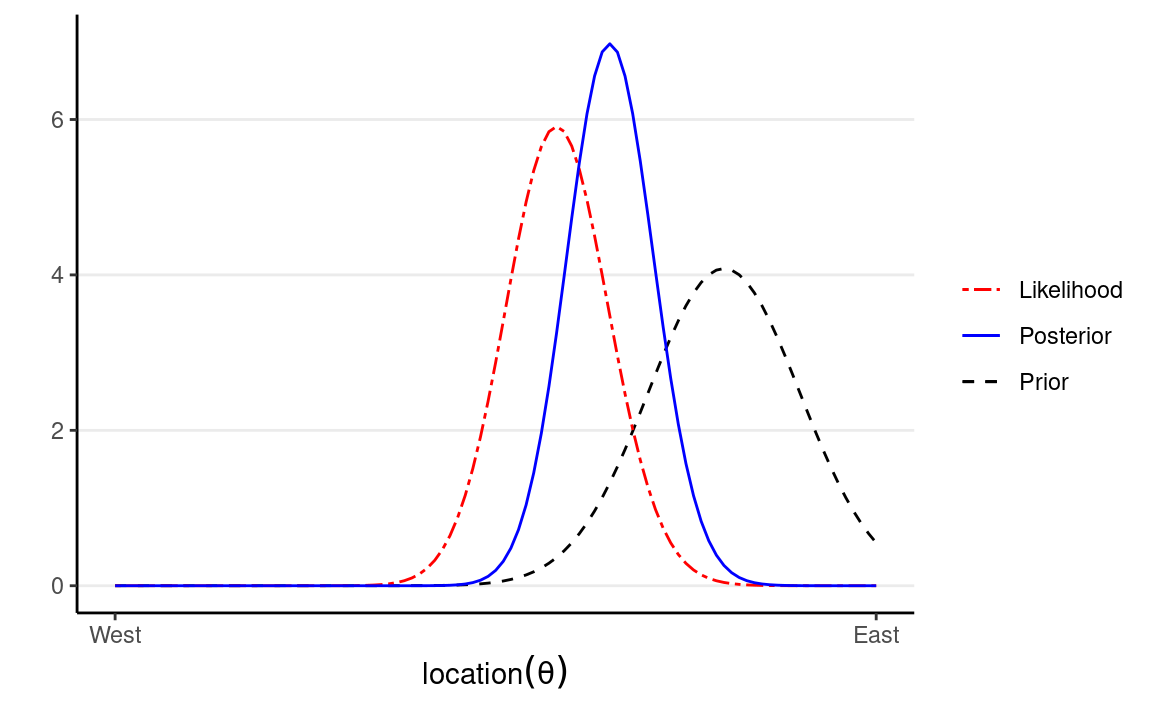
Influence of Prior

The following shows what happen with a stronger prior:

Influence of More Data

The following shows what happen with 20 more data points:

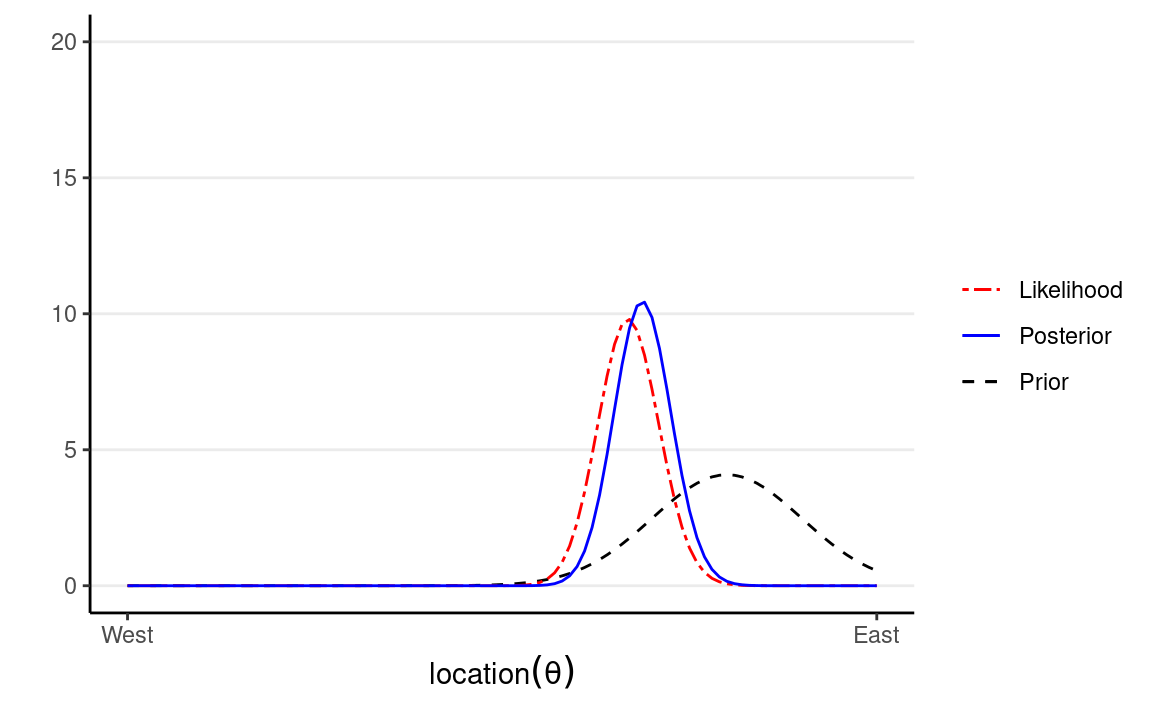
Data-Order Invariance

In many data analysis applications, researchers collect some data \(D_1\), and then collect some more data \(D_2\). An example would be researchers conducting two separate experiments to study the same research question. In Bayesian statistics, one can consider three ways to obtain the posterior:

  1. Update the belief with \(D_1\), and then with \(D_2\)
  2. Update the belief with \(D_2\), and then with \(D_1\)
  3. Update the belief with both \(D_1\) and \(D_2\) simultaneously

Whether these three ways give the same posterior depends on whether data-order invariance holds. If the inference of \(D_1\) does not depend on \(D_2\), or vice versa, then all three ways lead to the same posterior. Specifically, if we have conditional independence such that \[P(D_1, D_2 \mid \theta) = P(D_1 \mid \theta) P(D_2 \mid \theta),\] then one can show all three ways give the same posterior (see p. 108 of Kruschke, 2015).

Exchangeability*

Exchangeability is an important concept in Bayesian statistics. Data are exchangeable when the joint distribution, \(P(D_1, \ldots, D_N)\), does not depend on the ordering of the data. A simple way to think about it is if you scramble the order of your outcome variable in your data set and still can obtain the same statistical results, then the data are exchangeable. An example situation where data are not exchangeable is

When data are exchangeable, the previously discussed conditional independence condition would generally hold.2

Bernoulli Likelihood

For binary data \(y\) (e.g., coin flip, pass/fail, diagnosed/not), an intuitive way to analyze is to use a Bernoulli model: \[ \begin{aligned} P(y = 1 \mid \theta) = \theta \\ P(y = 0 \mid \theta) = 1 - \theta \end{aligned}, \] which is more compactly written as \[P(y \mid \theta) = \theta^y (1 - \theta)^{(1 - y)},\] where \(\theta \in [0, 1]\) is the probability of a “1”. You can verify that the compact form is the same as the longer form.

Multiple Observations

When there are more than one \(y\), say \(y_1, \ldots, y_N\), that are conditionally independent, we have \[ \begin{aligned} P(y_1, \ldots, y_N \mid \theta) & = \prod_{i = 1}^N P(y_i \mid \theta) \\ & = \theta^{\sum_{i = 1}^N y_i} (1 - \theta)^{\sum_{i = 1}^N (1 - y_i)} \\ & = \theta^z (1 - \theta)^{N - z} \end{aligned}, \] where \(z\) is the number of “1”s (e.g., number of heads in coin flips). Note that the likelihood only depends on \(z\), not the individual \(y\)s. In other words, the likelihood is the same as long as there are \(z\) heads, regardless of when those heads occur.

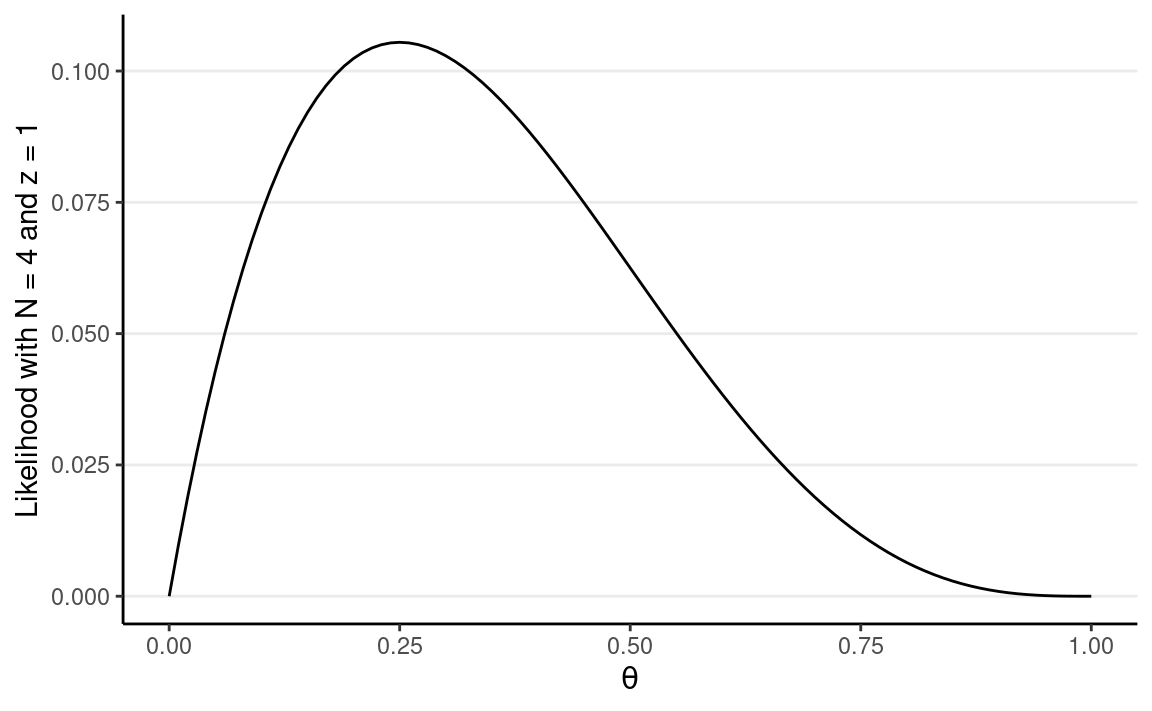
Let’s say \(N\) = 4 and \(z\) = 1. We can plot the likelihood in R:

# Write the likelihood as a function of theta
lik <- function(th, num_flips = 4, num_heads = 1) {
    th ^ num_heads * (1 - th) ^ (num_flips - num_heads)
}
# Likelihood of theta = 0.5
lik(0.5)

#> [1] 0.0625
# Plot the likelihood
ggplot(tibble(th = c(0, 1)), aes(x = th)) +
    # `stat_function` for plotting a function
    stat_function(fun = lik) +
    # use `expression()` to get greek letters
    labs(x = expression(theta),
    y = "Likelihood with N = 4 and z = 1")

Setting Priors

Remember again the relationship between the prior and the posterior: \[P(\theta | y) \propto P(y | \theta) P(\theta)\] The posterior distributions are mathematically determined once the priors and the likelihood are set. However, the mathematical form of the posterior is sometimes very difficult to deal with.

One straight forward, brute-force method is to discretize the parameter space into a number of points. For example, by taking \(\theta\) = 0, 0.05, 0.10, . . . , 0.90, 0.95, 1.00, one can evaluate the posterior at these 21 grid points.

Let’s use a prior that peaks at 0.5 and linearly decreases to both sides. I assume that \(\theta\) = 0.5 is twice as likely as \(\theta = 0.25\) or \(\theta = 0.75\) to reflect my belief that the coin is more likely to be fair.

# Define a grid for the parameter
grid_df <- tibble(th = seq(0, 1, by = 0.05))
# Set the prior mass for each value on the grid
grid_df$pth <- c(0:10, 9:0)  # linearly increasing, then decreasing
# Convert pth to a proper distribution such that the value
# sum to one
grid_df$pth <- grid_df$pth / sum(grid_df$pth)
# Plot the prior
ggplot(grid_df, aes(x = th, y = pth)) +
    geom_col(aes(x = th, y = pth),
        width = 0.01,
    ) +
    labs(y = expression(P(theta)), x = expression(theta))

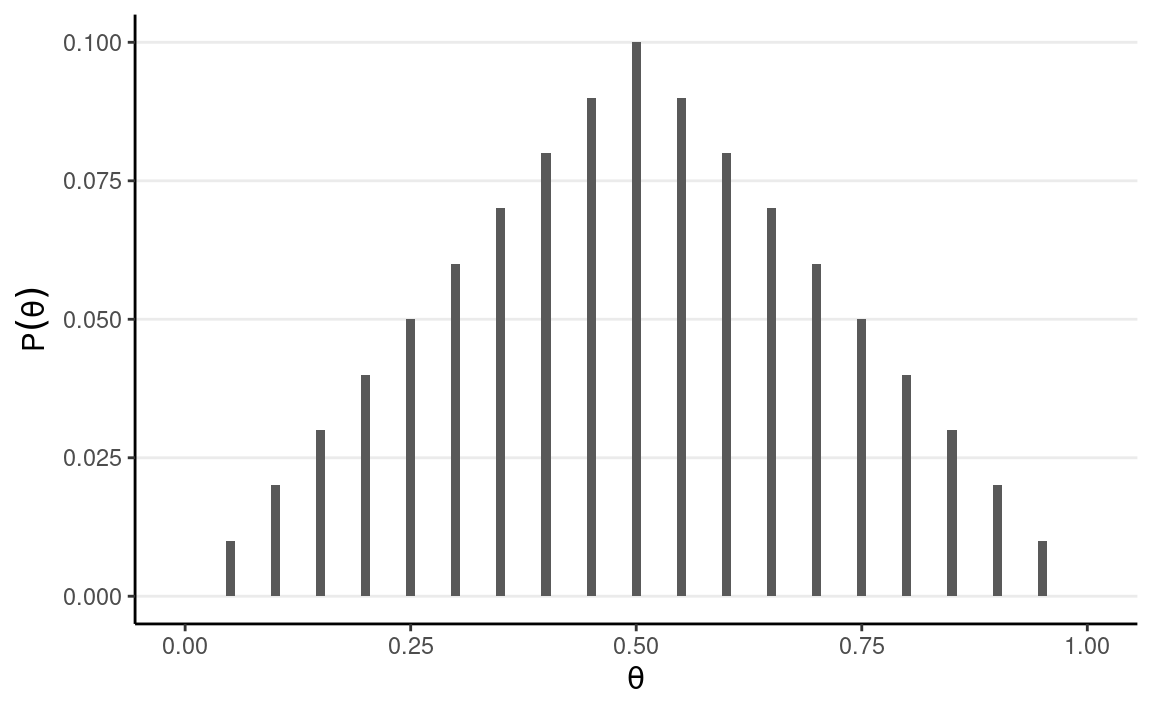
Note the line grid_df$pth <- grid_df$pth / sum(grid_df$pth), which ensures that the probability values sum to one. This is a trick we will use to obtain the posterior probability.

Prior Predictive Distribution

One way to check whether the prior is appropriate is to use the prior predictive distribution. Bayesian models are generative in the sense that they can be used to simulate data. The prior predictive distribution can be obtained by first simulating some \(\theta\) values from the prior distribution and then simulating a data set for each \(\theta\).

# Draw one theta
num_trials <- 4  # number of draws
sim_th1 <- sample(grid_df$th, size = 1,
                  # based on prior probability
                  prob = grid_df$pth)
# Simulate new data of four flips based on model
sim_y1 <- rbinom(num_trials, size = 1, prob = sim_th1)

# Repeat many times
# Set number of simulation draws
num_draws <- 1000
sim_th <- sample(grid_df$th, size = num_draws, replace = TRUE,
                 # based on prior probability
                 prob = grid_df$pth)
# Use a for loop
# Initialize output
sim_y <- matrix(NA, nrow = num_trials, ncol = num_draws)
for (s in seq_len(num_draws)) {
    # Store simulated data in the sth column
    sim_y[, s] <- rbinom(num_trials, size = 1, prob = sim_th[s])
}
# Show the first 10 simulated data sets based on prior:
sim_y[, 1:10]

#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#> [1,]    1    0    0    1    0    1    0    0    0     1
#> [2,]    0    0    0    1    1    0    1    0    1     1
#> [3,]    1    0    0    1    0    0    0    1    1     1
#> [4,]    1    0    1    1    1    0    0    1    1     0
# Show the distribution of number of heads
sim_heads <- colSums(sim_y)
ggplot(tibble(z = sim_heads), aes(x = z)) +
    geom_bar()

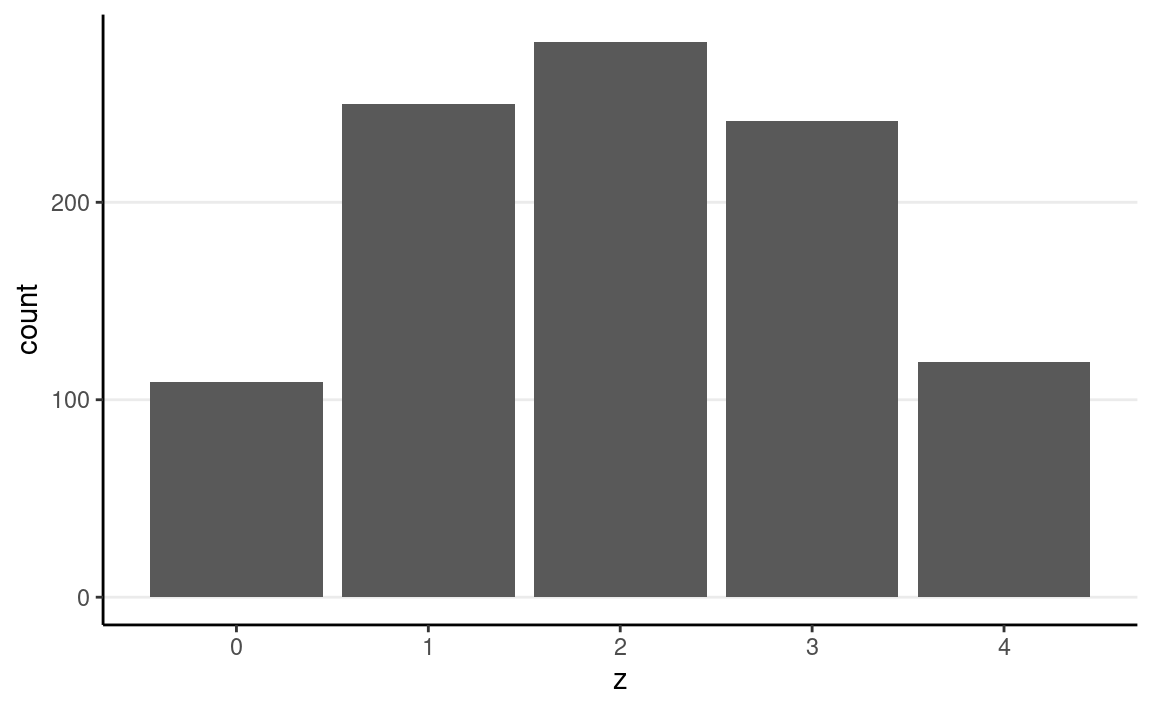
The outcome seems to fit our intuition that it’s more likely to be half heads and half tails, but there is a lot of uncertainty.

Summarizing the Posterior

grid_df <- grid_df %>%
    mutate(
        # Use our previously defined lik() function
        py_th = lik(th, num_flips = 4, num_heads = 1),
        # Product of prior and likelihood
        `prior x lik` = pth * py_th,
        # Scaled the posterior
        pth_y = `prior x lik` / sum(`prior x lik`)
    )
# Print a table
knitr::kable(grid_df)
th pth py_th prior x lik pth_y
0.00 0.00 0.0000000 0.0000000 0.0000000
0.05 0.01 0.0428687 0.0004287 0.0073359
0.10 0.02 0.0729000 0.0014580 0.0249500
0.15 0.03 0.0921188 0.0027636 0.0472914
0.20 0.04 0.1024000 0.0040960 0.0700927
0.25 0.05 0.1054688 0.0052734 0.0902416
0.30 0.06 0.1029000 0.0061740 0.1056525
0.35 0.07 0.0961187 0.0067283 0.1151381
0.40 0.08 0.0864000 0.0069120 0.1182815
0.45 0.09 0.0748688 0.0067382 0.1153071
0.50 0.10 0.0625000 0.0062500 0.1069530
0.55 0.09 0.0501187 0.0045107 0.0771891
0.60 0.08 0.0384000 0.0030720 0.0525695
0.65 0.07 0.0278687 0.0019508 0.0333832
0.70 0.06 0.0189000 0.0011340 0.0194056
0.75 0.05 0.0117188 0.0005859 0.0100268
0.80 0.04 0.0064000 0.0002560 0.0043808
0.85 0.03 0.0028687 0.0000861 0.0014727
0.90 0.02 0.0009000 0.0000180 0.0003080
0.95 0.01 0.0001187 0.0000012 0.0000203
1.00 0.00 0.0000000 0.0000000 0.0000000 
# Plot the prior/likelihood and the posterior
p1 <- ggplot(data = grid_df, aes(x = th)) +
    geom_col(aes(x = th - 0.005, y = pth, fill = "prior"),
        width = 0.01,
    ) +
    geom_col(aes(x = th + 0.005, y = py_th / sum(py_th),
        fill = "scaled likelihood"), width = 0.01,
    ) +
    labs(fill = NULL, y = NULL, x = expression(theta)) +
    theme(legend.position = "top")
p2 <- ggplot(data = grid_df, aes(x = th)) +
    geom_col(aes(x = th, y = pth_y), width = 0.01) +
    labs(
        fill = NULL, y = NULL, title = "Posterior",
        x = expression(theta)
    )
gridExtra::grid.arrange(p1, p2)

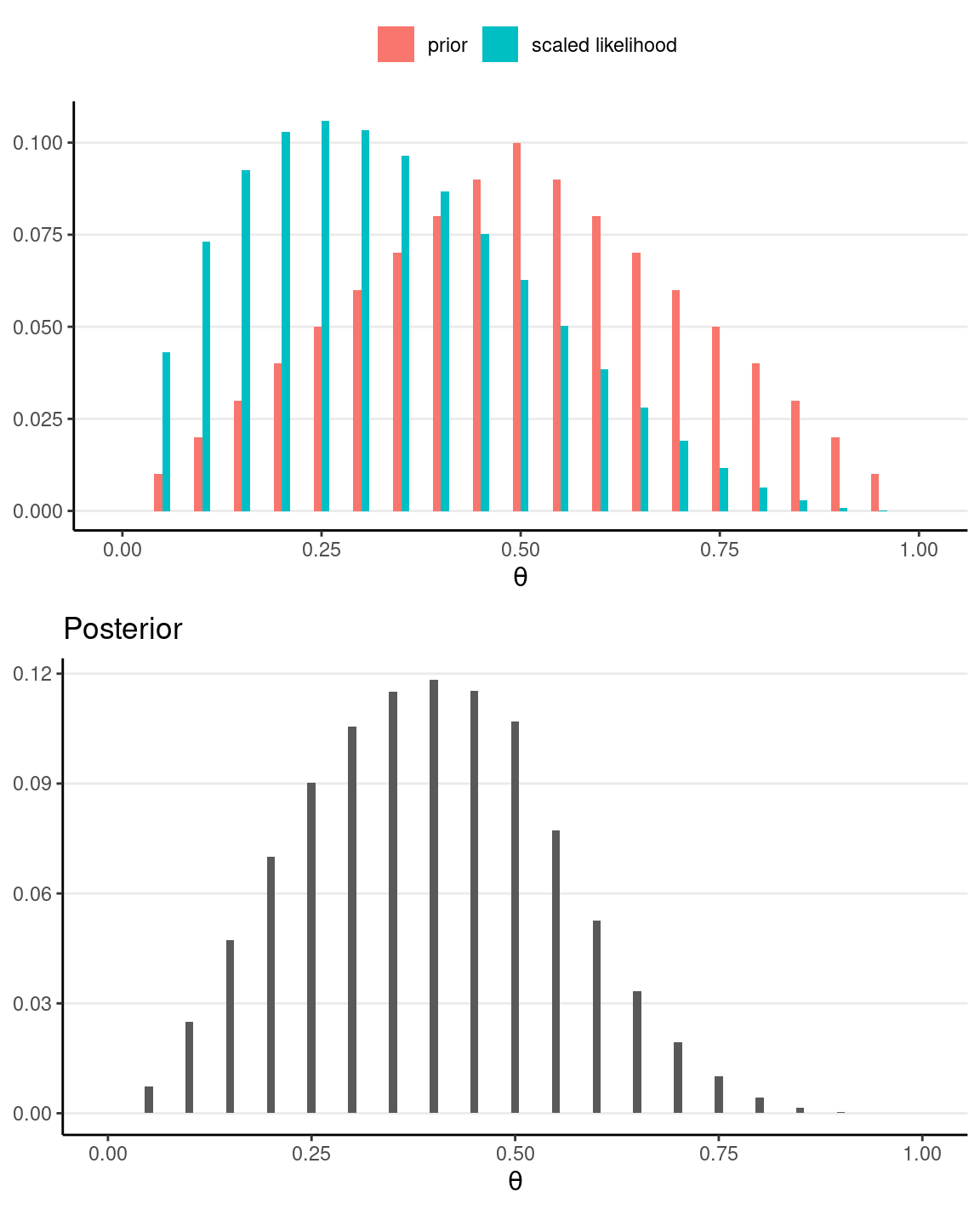
The second graph above shows the posterior distribution, which represents our updated belief about \(\theta\). We can summarize it by simulating \(\theta\) values from it and compute summary statistics:

# Define a function for computing posterior summary
summ_draw <- function(x) {
    c(
        mean = mean(x),
        median = median(x),
        sd = sd(x),
        mad = mad(x),
        `ci.1` = quantile(x, prob = .1, names = FALSE),
        `ci.9` = quantile(x, prob = .9, names = FALSE)
    )
}
# Sample from the posterior
post_samples <- sample(
    grid_df$th,
    size = 1000, replace = TRUE,
    prob = grid_df$pth_y
)
summ_draw(post_samples)

#>      mean    median        sd       mad      ci.1      ci.9 
#> 0.3848000 0.4000000 0.1538429 0.1482600 0.2000000 0.6000000

Influence of Sample Size

If, instead, we have \(N\) = 40 and \(z\) = 10, the posterior will be more similar to the likelihood.

grid_df2 <- grid_df %>%
    mutate(
        # Use our previously defined lik() function
        py_th = lik(th, num_flips = 40, num_heads = 10),
        # Product of prior and likelihood
        `prior x lik` = pth * py_th,
        # Scaled the posterior
        pth_y = `prior x lik` / sum(`prior x lik`)
    )
# Plot the prior/likelihood and the posterior
p1 <- ggplot(data = grid_df2, aes(x = th)) +
    geom_col(aes(x = th - 0.005, y = pth, fill = "prior"),
        width = 0.01,
    ) +
    geom_col(aes(x = th + 0.005, y = py_th / sum(py_th),
        fill = "scaled likelihood"), width = 0.01,
    ) +
    labs(fill = NULL, y = NULL, x = expression(theta)) +
    theme(legend.position = "top")
p2 <- ggplot(data = grid_df2, aes(x = th)) +
    geom_col(aes(x = th, y = pth_y), width = 0.01) +
    labs(
        fill = NULL, y = NULL, title = "Posterior",
        x = expression(theta)
    )
gridExtra::grid.arrange(p1, p2)


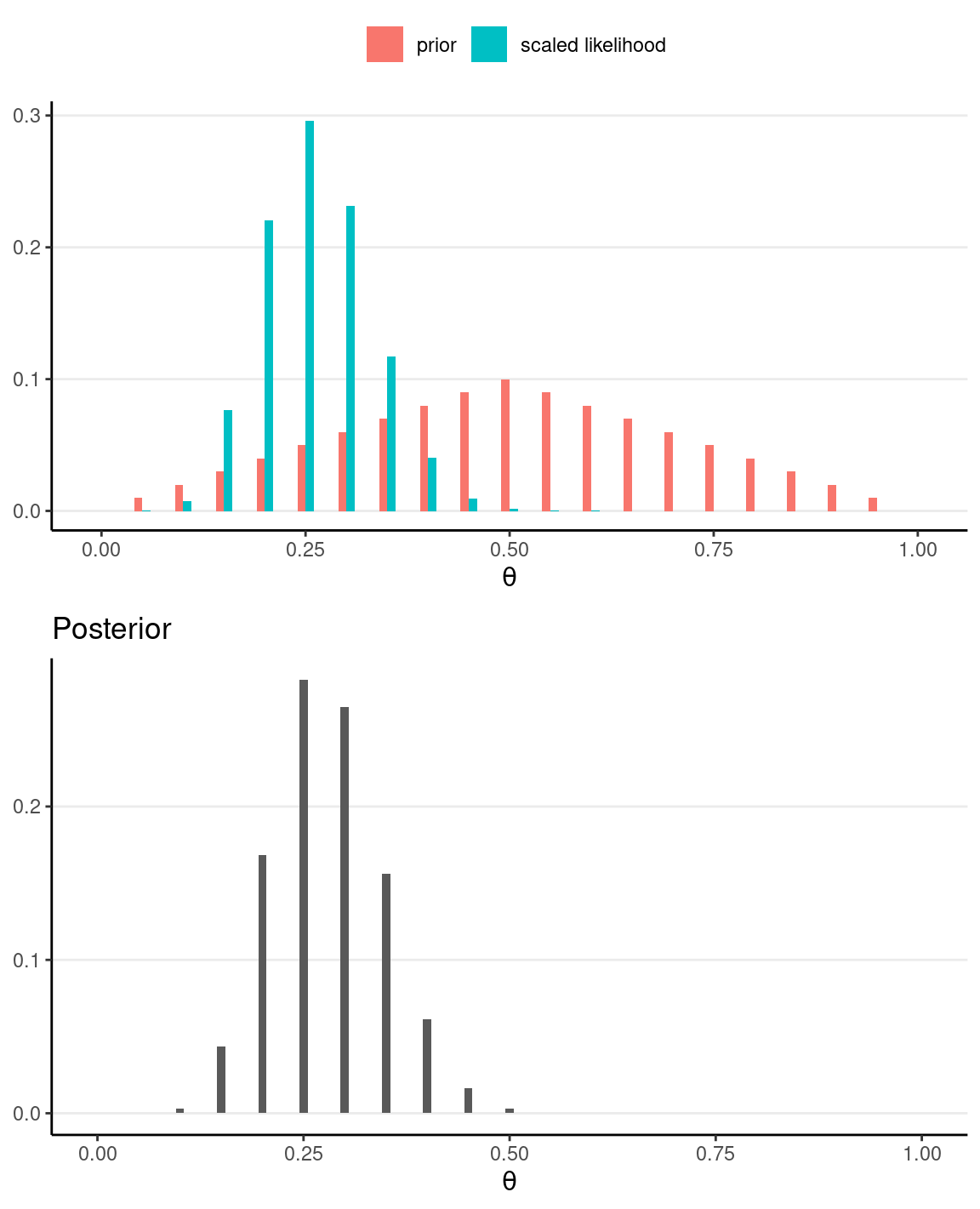
# Sample from the posterior
post_samples <- sample(
    grid_df2$th,
    size = 1000, replace = TRUE,
    prob = grid_df2$pth_y
)
summ_draw(post_samples)

#>       mean     median         sd        mad       ci.1       ci.9 
#> 0.28085000 0.30000000 0.06542215 0.07413000 0.20000000 0.35000000

Influence of Prior

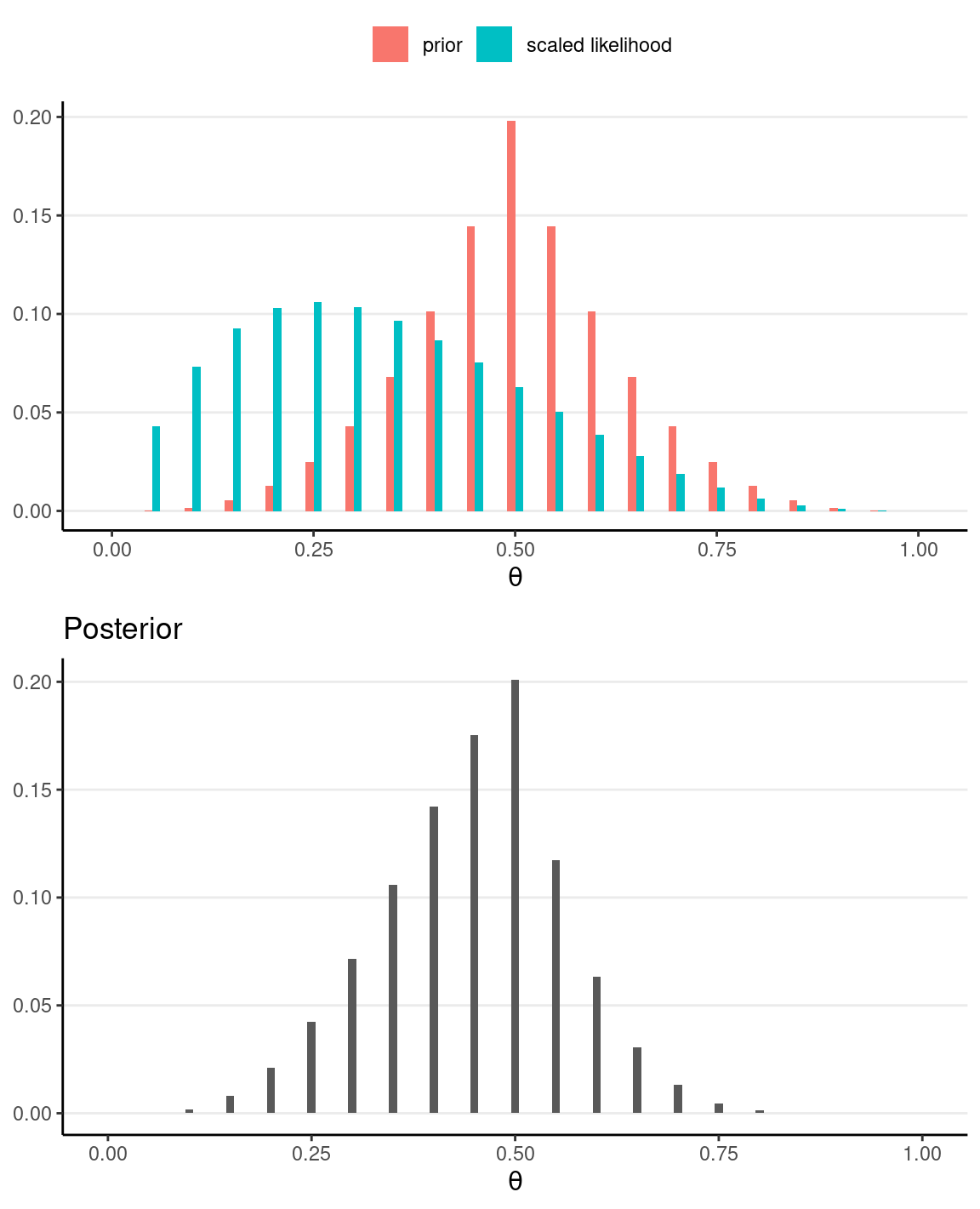
If we have a very strong prior concentrated at \(\theta\) = .5, but still with \(N\) = 40 and \(z\) = 10, the posterior will be more similar to the prior.

grid_df3 <- grid_df %>%
    mutate(
        # stronger prior
        pth = pth ^ 3,
        # scale the prior to sume to 1
        pth = pth / sum(pth),
        # Use our previously defined lik() function
        py_th = lik(th, num_flips = 4, num_heads = 1),
        # Product of prior and likelihood
        `prior x lik` = pth * py_th,
        # Scaled the posterior
        pth_y = `prior x lik` / sum(`prior x lik`)
    )
# Plot the prior/likelihood and the posterior
p1 <- ggplot(data = grid_df3, aes(x = th)) +
    geom_col(aes(x = th - 0.005, y = pth, fill = "prior"),
        width = 0.01,
    ) +
    geom_col(aes(x = th + 0.005, y = py_th / sum(py_th),
        fill = "scaled likelihood"), width = 0.01,
    ) +
    labs(fill = NULL, y = NULL, x = expression(theta)) +
    theme(legend.position = "top")
p2 <- ggplot(data = grid_df3, aes(x = th)) +
    geom_col(aes(x = th, y = pth_y), width = 0.01) +
    labs(
        fill = NULL, y = NULL, title = "Posterior",
        x = expression(theta)
    )
gridExtra::grid.arrange(p1, p2)


# Sample from the posterior
post_samples <- sample(
    grid_df3$th,
    size = 1000, replace = TRUE,
    prob = grid_df3$pth_y
)
summ_draw(post_samples)

#>      mean    median        sd       mad      ci.1      ci.9 
#> 0.4493000 0.4500000 0.1096656 0.0741300 0.3000000 0.6000000

Remark on Grid Approximation

In this note, we discretized \(\theta\) into a finite number of grid points to compute the posterior, mainly for pedagogical purposes. A big limitation is that our posterior will have no density for values other than the chosen grid points. While increasing the number of grid points (e.g., 1,000) can give more precision, the result is still not truly continuous. A bigger issue is that the computation breaks down when there is more than one parameter; if there are \(p\) parameters, with 1,000 grid points per parameter, one needs to evaluate the posterior probability for \(1,000^p\) grid points, which is not feasible even with modern computers. So more efficient algorithms, namely Markov chain Monte Carlo (MCMC) methods, will be introduced as we progress in the course.

Last updated

#> [1] "January 22, 2022"

  1. The likelihood function in classical/frequentist statistics is usually written as \(P(y; \theta)\). You will notice that here I write the likelihood for classical/frequentist statistics to be different from the one used in Bayesian statistics. This is intentional: In frequentist conceptualization, \(\theta\) is fixed, and it does not make sense to talk about the probability of \(\theta\). This implies that we cannot condition on \(\theta\), because conditional probability is defined only when \(P(\theta)\) is defined.↩︎

  2. The de Finetti’s theorem shows that when the data are exchangeable and can be considered an infinite sequence (i.e., not from a tiny finite population), then the data are conditionally independent given some \(\theta\).↩︎

Corrections

If you see mistakes or want to suggest changes, please create an issue on the source repository.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY-NC-SA 4.0. Source code is available at https://github.com/marklhc/20221-psyc573-usc, unless otherwise noted. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".

© Copyright 2022 Hok Chio (Mark) Lai

Template by The Distill Template Authors and RStudio, Inc.