+ - 0:00:00
Notes for current slide
Notes for next slide

Hierarchical Models

PSYC 573

University of Southern California

March 3, 2022

1 / 22

Therapeutic Touch Example (N = 28)

2 / 22

Data Points From One Person

y: whether the guess of which hand was hovered over was correct

Person S01

y s
1 S01
0 S01
0 S01
0 S01
0 S01
0 S01
0 S01
0 S01
0 S01
0 S01
3 / 22

Binomial Model

We can use a Bernoulli model: yi∼Bern(θ) for i=1,…,N

4 / 22

Binomial Model

We can use a Bernoulli model: yi∼Bern(θ) for i=1,…,N

Assuming exchangeability given θ, more succint to write z∼Bin(N,θ) for z=∑i=1Nyi

4 / 22

Binomial Model

We can use a Bernoulli model: yi∼Bern(θ) for i=1,…,N

Assuming exchangeability given θ, more succint to write z∼Bin(N,θ) for z=∑i=1Nyi

  • Bernoulli: Individual trial
  • Binomial: total count of "1"s
4 / 22

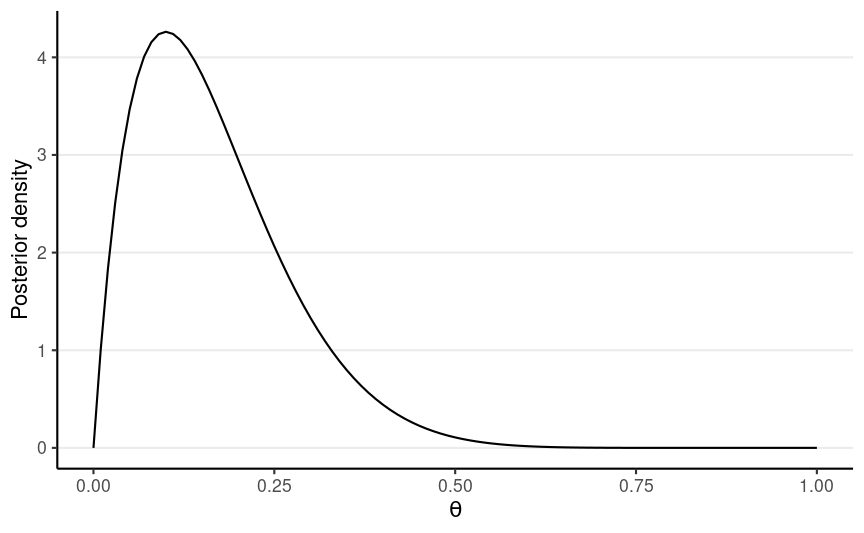
1 success, 9 failures

Posterior: Beta(2, 10)

5 / 22

Multiple People

We could repeat the binomial model for each of the 28 participants, to obtain posteriors for θ1, …, θ28

But . . .

6 / 22

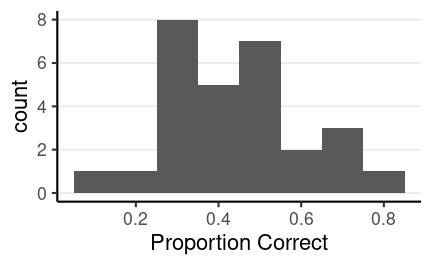
We'll continue the therapeutic touch example. To recap, we have 28 participants, each of them go through 10 trials to guess which of their hands was hovered above. The histogram shows the distribution of the proportion correct.

Multiple People

We could repeat the binomial model for each of the 28 participants, to obtain posteriors for θ1, …, θ28

But . . .

Do we think our belief about θ1 would inform our belief about θ2, etc?

6 / 22

We'll continue the therapeutic touch example. To recap, we have 28 participants, each of them go through 10 trials to guess which of their hands was hovered above. The histogram shows the distribution of the proportion correct.

Multiple People

We could repeat the binomial model for each of the 28 participants, to obtain posteriors for θ1, …, θ28

But . . .

Do we think our belief about θ1 would inform our belief about θ2, etc?

After all, human beings share 99.9% of genetic makeup

6 / 22

We'll continue the therapeutic touch example. To recap, we have 28 participants, each of them go through 10 trials to guess which of their hands was hovered above. The histogram shows the distribution of the proportion correct.

Three Positions of Pooling

  • No pooling: each individual is completely different; inference of θ1 should be independent of θ2, etc

  • Complete pooling: each individual is exactly the same; just one θ instead of 28 θj's

  • Partial pooling: each individual has something in common but also is somewhat different

7 / 22

No Pooling

boxes_and_circles th1 θ 1 y1 y 1 th1->y1 th2 θ 2 y2 y 2 th2->y2 th3 ... th4 θ J - 1 y4 y J - 1 th4->y4 th5 θ J y5 y J th5->y5 y3 ...
8 / 22

Complete Pooling

boxes_and_circles th θ y1 y 1 th->y1 y2 y 2 th->y2 y4 y J - 1 th->y4 y5 y J th->y5 y3 ...
9 / 22

Partial Pooling

boxes_and_circles hy μ, κ th1 θ 1 hy->th1 th2 θ 2 hy->th2 th4 θ J - 1 hy->th4 th5 θ J hy->th5 y1 y 1 th1->y1 y2 y 2 th2->y2 th3 ... y4 y J - 1 th4->y4 y5 y J th5->y5 y3 ...
10 / 22

Partial Pooling in Hierarchical Models

Hierarchical Priors: θj∼Beta2(μ,κ)

Beta2: reparameterized Beta distribution

  • mean μ=a/(a+b)
  • concentration κ=a+b

Expresses the prior belief:

Individual θs follow a common Beta distribution with mean μ and concentration κ

11 / 22

How to Choose κ

If κ→∞: everyone is the same; no individual differences (i.e., complete pooling)

If κ=0: everybody is different; nothing is shared (i.e., no pooling)

12 / 22

How to Choose κ

If κ→∞: everyone is the same; no individual differences (i.e., complete pooling)

If κ=0: everybody is different; nothing is shared (i.e., no pooling)

We can fix a κ value based on our belief of how individuals are similar or different

12 / 22

How to Choose κ

If κ→∞: everyone is the same; no individual differences (i.e., complete pooling)

If κ=0: everybody is different; nothing is shared (i.e., no pooling)

We can fix a κ value based on our belief of how individuals are similar or different

A more Bayesian approach is to treat κ as an unknown, and use Bayesian inference to update our belief about κ

12 / 22

Generic prior by Kruschke (2015): κ ∼ Gamma(0.01, 0.01)

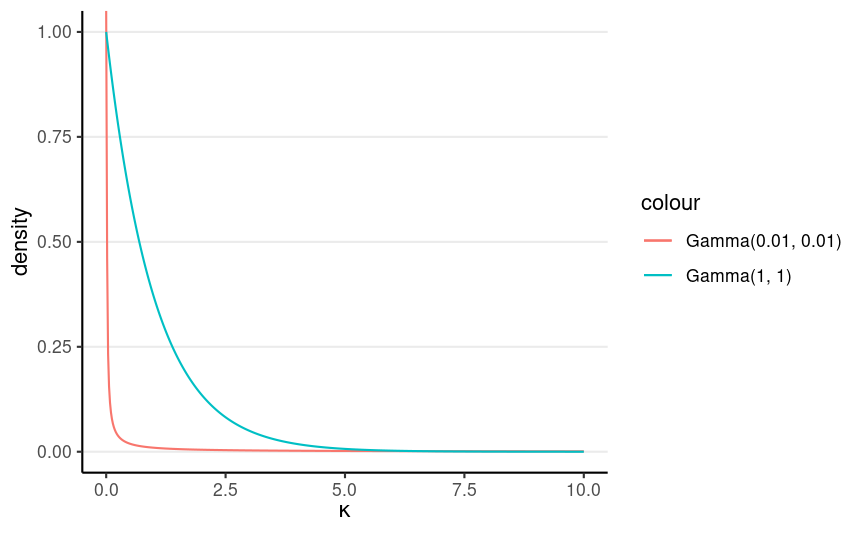
Sometimes you may want a stronger prior like Gamma(1, 1), if it is unrealistic to do no pooling

13 / 22

Full Model

Model: zj∼Bin(Nj,θj)θj∼Beta2(μ,κ) Prior: μ∼Beta(1.5,1.5)κ∼Gamma(0.01,0.01)

data {
  int<lower=0> J;         // number of clusters (e.g., studies, persons)
  int y[J];               // number of "1"s in each cluster
  int N[J];               // sample size for each cluster
}
parameters {
  vector<lower=0, upper=1>[J] theta;   // cluster-specific probabilities
  real<lower=0, upper=1> mu;     // overall mean probability
  real<lower=0> kappa;           // overall concentration
}
model {
  y ~ binomial(N, theta);              // each observation is binomial
  theta ~ beta_proportion(mu, kappa);  // prior; Beta2 dist
  mu ~ beta(1.5, 1.5);           // weak prior
  kappa ~ gamma(.01, .01);       // prior recommended by Kruschke
}
14 / 22

Here is the Stan code. The inputs are J, the number of people, y, which is actually z in our model for the individual counts, but I use y just because y is usually the outcome in Stan. N is the number of trials per person, and here N[J] means the number of trials can be different across individuals.

The parameters and the model block pretty much follow the mathematical model. The beta_proportion() function is what I said Beta2 as the beta distribution with the mean and the concentration as the parameters.

You may want to pause here to make sure you understand the Stan code.

Posterior of Hyperparameters

library(bayesplot)
mcmc_dens(tt_fit, pars = c("mu", "kappa"))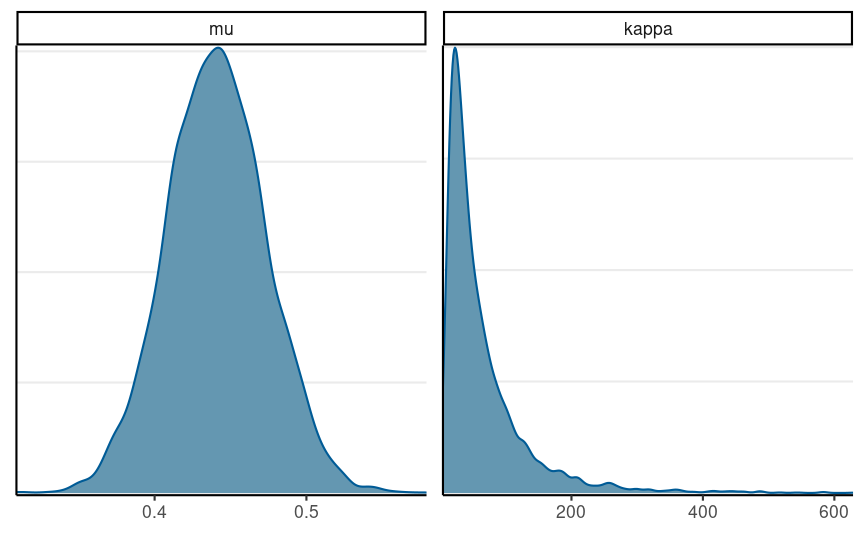

15 / 22

The graphs show the posterior for mu and kappa. As you can see, the average probability of guessing correctly has most density between .4 and .5.

For kappa, the posterior has a pretty long tail, and the value of kappa being very large, like 100 or 200, is pretty likely. So this suggests the individuals may be pretty similar to each other.

Shrinkage

16 / 22

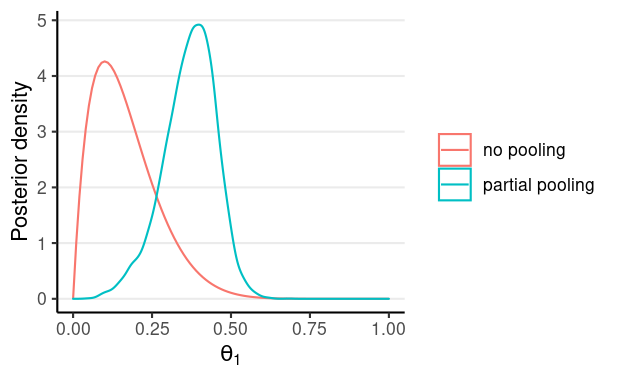
From the previous model, we get posterior distributions for all parameters, including mu, kappa, and 28 thetas. The first graph shows the posterior for theta for person 1. The red curve is the one without any pooling, so the distribution is purely based on the 10 trials for person 1. The blue curve, on the other hand, is much closer to .5 due to partial pooling. Because the posterior of kappa is pretty large, the posterior is pooled towards the grand mean, mu.

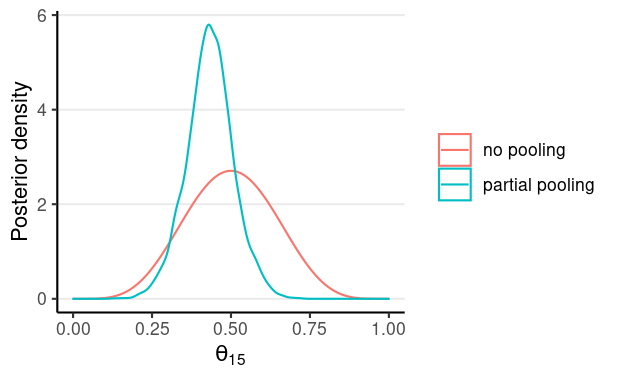
For the graph below, the posterior mean is close to .5 with or without partial pooling, but the distribution is narrower with partial pooling, which reflects a stronger belief. This is because, with partial pooling, the posterior distribution uses more information than just the 10 trials of person 15; it also borrows information from the other 27 individuals.

Multiple Comparisons?

Frequentist: family-wise error rate depends on the number of intended contrasts

17 / 22

One advantage of the hierarchical model is it is a solution to the multiple comparison problem. In frequentist analysis, if you have multiple groups, and you want to test each contrast, you will need to consider family-wise error rate, and do something like Bonferroni corrections.

Multiple Comparisons?

Frequentist: family-wise error rate depends on the number of intended contrasts

‍Bayesian: only one posterior; hierarchical priors already express the possibility that groups are the same

17 / 22

One advantage of the hierarchical model is it is a solution to the multiple comparison problem. In frequentist analysis, if you have multiple groups, and you want to test each contrast, you will need to consider family-wise error rate, and do something like Bonferroni corrections.

The Bayesian alternative is to do a hierarchial model with partial pooling. With Bayesian, you have one posterior distribution, which is the joint distribution of all parameters. And the use of a common distribution of the thetas already assigns some probability to the prior belief that the groups are the same.

Multiple Comparisons?

Frequentist: family-wise error rate depends on the number of intended contrasts

‍Bayesian: only one posterior; hierarchical priors already express the possibility that groups are the same

Thus, Bayesian hierarchical model "completely solves the multiple comparisons problem."1

[1]: see https://statmodeling.stat.columbia.edu/2016/08/22/bayesian-inference-completely-solves-the-multiple-comparisons-problem/

[2]: See more in ch 11.4 of Kruschke (2015)

17 / 22

One advantage of the hierarchical model is it is a solution to the multiple comparison problem. In frequentist analysis, if you have multiple groups, and you want to test each contrast, you will need to consider family-wise error rate, and do something like Bonferroni corrections.

The Bayesian alternative is to do a hierarchial model with partial pooling. With Bayesian, you have one posterior distribution, which is the joint distribution of all parameters. And the use of a common distribution of the thetas already assigns some probability to the prior belief that the groups are the same.

Therefore, with a hierarchical model, you can obtain the posterior of the difference of any groups, without worrying about how many comparisons you have conducted. You can read more in the sources listed here.

Hierarchical Normal Model

18 / 22

In this video, we'll talk about another Bayesian hierarchical model, the hierarchical normal model.

Effect of coaching on SAT-V

School Treatment Effect Estimate Standard Error
A 28 15
B 8 10
C -3 16
D 7 11
E -1 9
F 1 11
G 18 10
H 12 18
19 / 22

The data come from the 1980s when scholars were debating the effect of coaching on standardized tests. The test of interest is the SAT verbal subtest. The note contains more description of it.

The analysis will be on the secondary data from eight schools, from school A to school H. Each schools conducts its own randomized trial. The middle column shows the treatment effect estimate for the effect of coaching. For example, for school A, we see that students with coaching outperformed students without coaching by 28 points. However, for schools C and E, the effects were smaller and negative.

Finally, in the last column, we have the standard error of the treatment effect for each school, based on a t-test. As you know, the smaller the standard error, the less uncertainty we have on the treatment effect.

Model: dj∼N(θj,sj)θj∼N(μ,τ) Prior: μ∼N(0,100)τ∼t4+(0,100)

data {
  int<lower=0> J;          // number of schools 
  real y[J];               // estimated treatment effects
  real<lower=0> sigma[J];  // s.e. of effect estimates 
}
parameters {
  real mu;                 // overall mean
  real<lower=0> tau;       // between-school SD
  vector[J] eta;           // standardized deviation (z score)
}
transformed parameters {
  vector[J] theta;
  theta = mu + tau * eta;   // non-centered parameterization
}
model {
  eta ~ std_normal();       // same as eta ~ normal(0, 1);
  y ~ normal(theta, sigma);
  // priors
  mu ~ normal(0, 100);
  tau ~ student_t(4, 0, 100);
}
20 / 22

Individual-School Treatment Effects

21 / 22

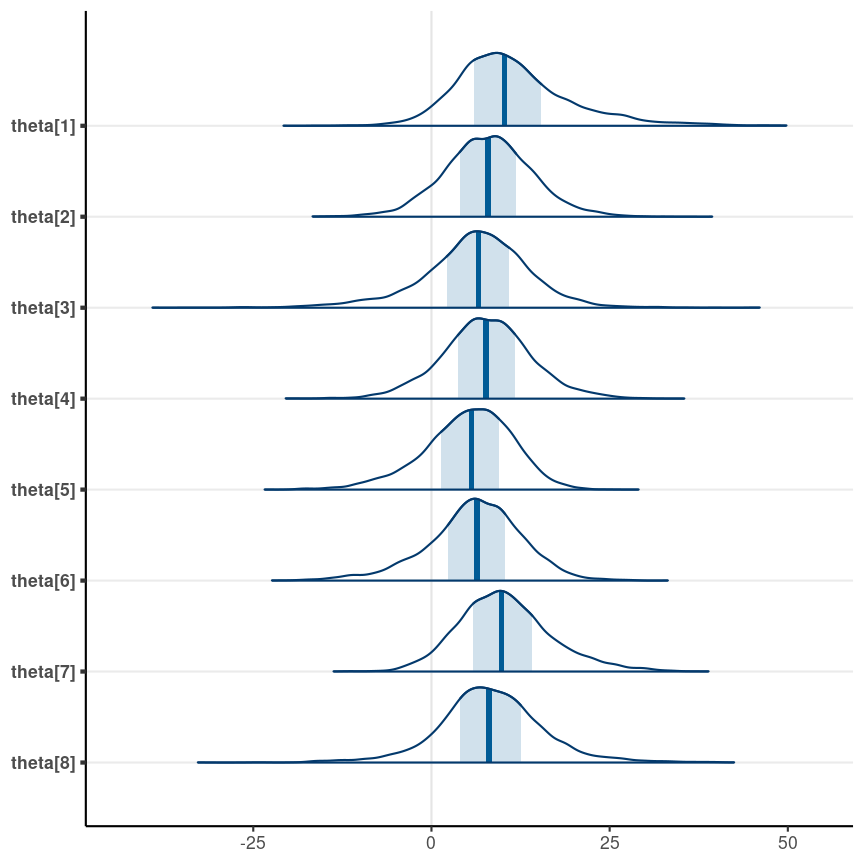
Prediction Interval

Posterior distribution of the true effect size of a new study, θ~

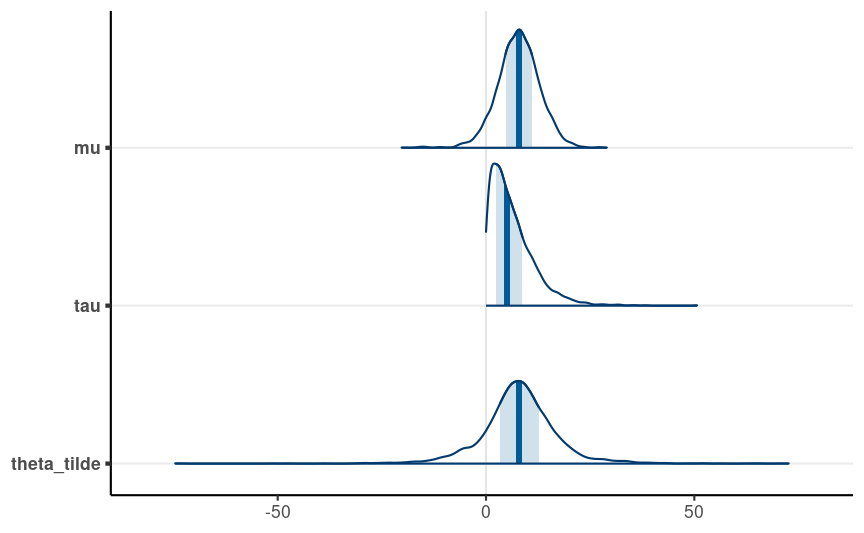
See https://onlinelibrary.wiley.com/doi/abs/10.1002/jrsm.12 for an introductory paper on random-effect meta-analysis

22 / 22

Therapeutic Touch Example (N = 28)

2 / 22
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow