Markov Chain Monte Carlo IIPSYC 573University of Southern CaliforniaFebruary 17, 20221 / 10

Markov Chain Monte Carlo II

PSYC 573

University of Southern California

February 17, 2022

What has been useful?

R command, exercises

1 / 10

Markov Chain Monte Carlo II

PSYC 573

University of Southern California

February 17, 2022

What has been useful?

R command, exercises

Struggles/Suggestion?

Download Rmd from website
Math concepts
More R code (especially related to the homework)

1 / 10

Markov Chain Monte Carlo II

PSYC 573

University of Southern California

February 17, 2022

What has been useful?

R command, exercises

Struggles/Suggestion?

Download Rmd from website
Math concepts
More R code (especially related to the homework)

Changes

Speed up a bit
Zoom
More time in R

1 / 10

The original Metropolis (random walk) algorithm allows posterior sampling, without the need to solving the integral

2 / 10

The original Metropolis (random walk) algorithm allows posterior sampling, without the need to solving the integral

However, it is inefficient, especially in high dimension problems (i.e., many parameters)

2 / 10

Data Example

Taking notes with a pen or a keyboard?

3 / 10

Mueller & Oppenheimer (2014, Psych Science)

# Use haven::read_sav() to import SPSS data
nt_dat <- haven::read_sav("https://osf.io/qrs5y/download")

0 = laptop, 1 = longhand

condition	wordcount	objectiveZ	openZ
0	572	-1.175	0.111
0	226	0.317	-0.864
0	255	-1.175	-0.376
0	298	1.063	1.086
1	203	-1.921	-0.376
1	127	-0.056	0.111
1	258	0.690	0.111
1	152	-0.429	0.599

4 / 10

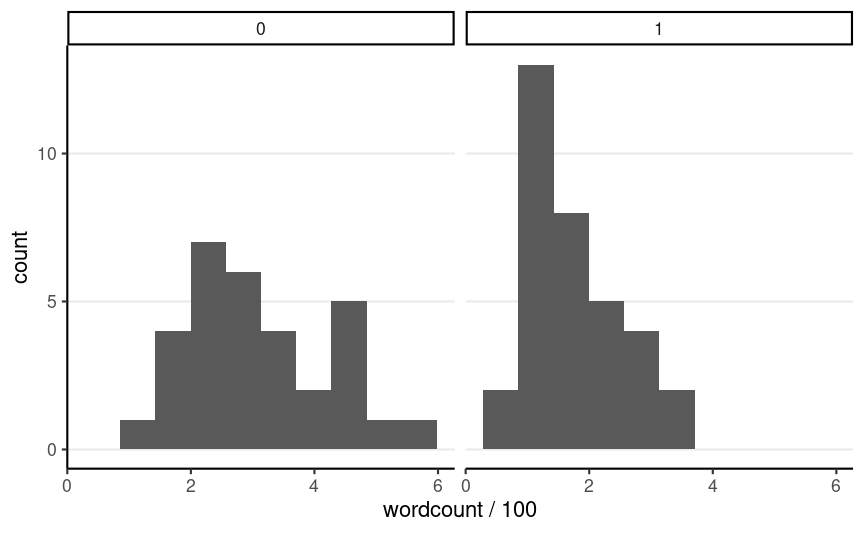
Do people write more or less words when asked to use longhand?

Normal model

Consider only the laptop group first

${wc_laptop}_{i} \sim N (μ, σ^{2})$ Two parameters: $μ$ (mean), $σ^{2}$ (variance)

5 / 10

Gibbs Sampling6 / 10

Gibbs sampling is efficient by generating smart proposed values, using conjugate or semiconjugate priors

Implemented in software like BUGS and JAGS

7 / 10

Gibbs sampling is efficient by generating smart proposed values, using conjugate or semiconjugate priors

Implemented in software like BUGS and JAGS

Useful when:

Joint posterior is intractable, but the conditional distributions are known

7 / 10

Another example

8 / 10

Conjugate priors for conditional distributions

$\begin{aligned} μ & \sim N (μ_{0}, τ_{0}^{2}) \\ σ^{2} & \sim Inv-Gamma (ν_{0} / 2, ν_{0} σ_{0}^{2} / 2) \end{aligned}$

$μ_{0}$ : Prior mean, $τ_{0}^{2}$ ; Prior variance (i.e., uncertainty) of the mean
$ν_{0}$ : Prior sample size for the variance; $σ_{0}^{2}$ : Prior expectation of the variance

Posterior

$\begin{aligned} μ ∣ σ^{2}, y & \sim N (μ_{n}, τ_{n}^{2}) \\ σ^{2} ∣ μ & \sim Inv-Gamma (ν_{n} / 2, ν_{n} σ_{n}^{2} [μ] / 2) \end{aligned}$

$τ_{n}^{2} = {(\frac{1}{τ_{0}^{2}} + \frac{n}{σ^{2}})}^{- 1}$ ; $μ_{n} = τ_{n}^{2} (\frac{μ_{0}}{τ_{0}^{2}} + \frac{n \bar{y}}{σ^{2}})$
$ν_{n} = ν_{0} + n$ ; $σ_{n}^{2} (μ) = \frac{1}{ν_{n}} [ν_{0} σ_{0}^{2} + (n - 1) s_{y}^{2} + \sum (\bar{y} - μ)^{2}]$

9 / 10

No need for a separate proposal distribution; directly sample the conditional posterior

Thus, all draws are accepted

10 / 10

No need for a separate proposal distribution; directly sample the conditional posterior

Thus, all draws are accepted

Posterior Summary

2 chains, 10,000 draws each, half warm-ups

$μ_{0}$ = 5, $σ_{0}^{2}$ = 1, $τ_{0}^{2}$ = 100, $ν_{0}$ = 1

variable	mean	median	sd	mad	q5	q95	rhat	ess_bulk	ess_tail
mu	3.1	3.10	0.213	0.211	2.753	3.45	1	9928	9936
sigma2	1.4	1.33	0.378	0.337	0.904	2.11	1	10189	10136

The ESS is almost as large as # of draws

10 / 10

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help