class: center, middle, inverse, title-slide # Markov Chain Monte Carlo II ## PSYC 573 ### University of Southern California ### February 17, 2022 --- exclude: TRUE # Mid-Semester Feedback Thanks for sharing your thoughts! - `\(n\)` = 10 -- What has been useful? - R command, exercises -- Struggles/Suggestion? - Download Rmd from website - Math concepts - More R code (especially related to the homework) --- exclude: TRUE class: clear Questions? - Psychology examples - Posterior predictive check - Beta likelihood; law of total probability (from conditional to marginal) - HW 3 ... -- Changes - Speed up a bit - Zoom - More time in R --- class: clear <style>.shareagain-bar { --shareagain-foreground: rgb(255, 255, 255); --shareagain-background: rgba(0, 0, 0, 0.5); --shareagain-twitter: none; --shareagain-facebook: none; --shareagain-linkedin: none; --shareagain-pinterest: none; --shareagain-pocket: none; --shareagain-reddit: none; }</style> The original Metropolis (random walk) algorithm allows posterior sampling, without the need to solving the integral -- However, it is inefficient, especially in high dimension problems (i.e., many parameters) --- class: inverse, middle, center # Data Example Taking notes with a pen or a keyboard? --- class: clear ### Mueller & Oppenheimer (2014, Psych Science) .panelset[ .panel[.panel-name[R code] ```r # Use haven::read_sav() to import SPSS data nt_dat <- haven::read_sav("https://osf.io/qrs5y/download") ``` ] .panel[.panel-name[Data] .font70[ 0 = laptop, 1 = longhand | condition| wordcount| objectiveZ| openZ| |---------:|---------:|----------:|------:| | 0| 572| -1.175| 0.111| | 0| 226| 0.317| -0.864| | 0| 255| -1.175| -0.376| | 0| 298| 1.063| 1.086| | 1| 203| -1.921| -0.376| | 1| 127| -0.056| 0.111| | 1| 258| 0.690| 0.111| | 1| 152| -0.429| 0.599| ] ] .panel[.panel-name[Histograms] <img src="gibbs_files/figure-html/hist-wordcount-1.png" width="70%" style="display: block; margin: auto;" /> ] ] --- class: clear > 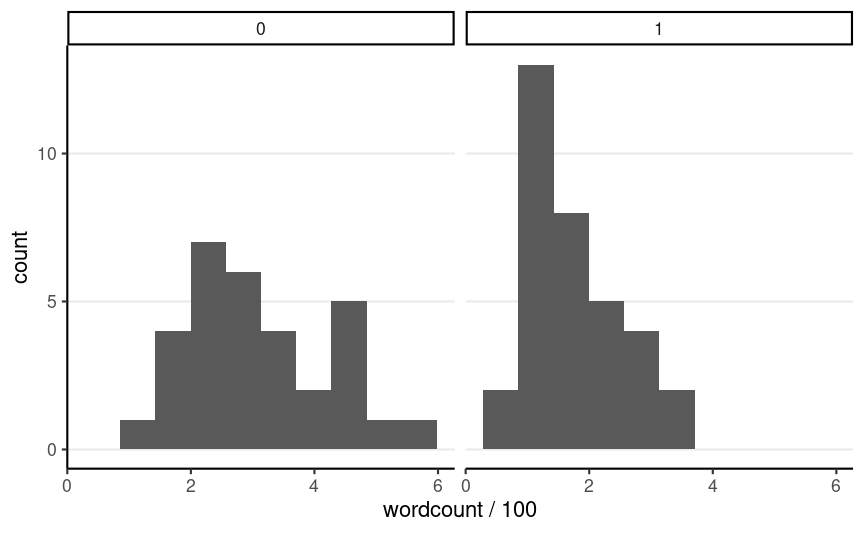Do people write more or less words when asked to use longhand? ### Normal model Consider only the laptop group first `$$\text{wc_laptop}_i \sim N(\mu, \sigma^2)$$` Two parameters: `\(\mu\)` (mean), `\(\sigma^2\)` (variance) --- class: inverse, middle, center # Gibbs Sampling --- class: clear Gibbs sampling is efficient by generating smart proposed values, using **conjugate** or **semiconjugate** priors Implemented in software like BUGS and JAGS -- Useful when: - Joint posterior is intractable, but the **conditional distributions** are known --- exclude: TRUE # Conditional Distributions <div id="htmlwidget-5ffcac17cd05f1513722" style="width:90%;height:432px;" class="plotly html-widget"></div> <script type="application/json" data-for="htmlwidget-5ffcac17cd05f1513722">{"x":{"visdat":{"ac482ff3300":["function () ","plotlyVisDat"]},"cur_data":"ac482ff3300","attrs":{"ac482ff3300":{"x":{},"y":{},"z":{},"alpha_stroke":1,"sizes":[10,100],"spans":[1,20],"type":"surface"}},"layout":{"margin":{"b":40,"l":60,"t":25,"r":10},"scene":{"xaxis":{"title":"sigma2_grid"},"yaxis":{"title":"mu_grid"},"zaxis":{"title":"grid_density"}},"hovermode":"closest","showlegend":false,"legend":{"yanchor":"top","y":0.5}},"source":"A","config":{"modeBarButtonsToAdd":["hoverclosest","hovercompare"],"showSendToCloud":false},"data":[{"colorbar":{"title":"grid_density","ticklen":2,"len":0.5,"lenmode":"fraction","y":1,"yanchor":"top"},"colorscale":[["0","rgba(68,1,84,1)"],["0.0416666666666667","rgba(70,19,97,1)"],["0.0833333333333333","rgba(72,32,111,1)"],["0.125","rgba(71,45,122,1)"],["0.166666666666667","rgba(68,58,128,1)"],["0.208333333333333","rgba(64,70,135,1)"],["0.25","rgba(60,82,138,1)"],["0.291666666666667","rgba(56,93,140,1)"],["0.333333333333333","rgba(49,104,142,1)"],["0.375","rgba(46,114,142,1)"],["0.416666666666667","rgba(42,123,142,1)"],["0.458333333333333","rgba(38,133,141,1)"],["0.5","rgba(37,144,140,1)"],["0.541666666666667","rgba(33,154,138,1)"],["0.583333333333333","rgba(39,164,133,1)"],["0.625","rgba(47,174,127,1)"],["0.666666666666667","rgba(53,183,121,1)"],["0.708333333333333","rgba(79,191,110,1)"],["0.75","rgba(98,199,98,1)"],["0.791666666666667","rgba(119,207,85,1)"],["0.833333333333333","rgba(147,214,70,1)"],["0.875","rgba(172,220,52,1)"],["0.916666666666667","rgba(199,225,42,1)"],["0.958333333333333","rgba(226,228,40,1)"],["1","rgba(253,231,37,1)"]],"showscale":true,"x":[0.5,0.58,0.66,0.74,0.82,0.9,0.98,1.06,1.14,1.22,1.3,1.38,1.46,1.54,1.62,1.7,1.78,1.86,1.94,2.02,2.1,2.18,2.26,2.34,2.42,2.5,2.58,2.66,2.74,2.82,2.9,2.98,3.06,3.14,3.22,3.3,3.38,3.46,3.54,3.62,3.7,3.78,3.86,3.94,4.02,4.1,4.18,4.26,4.34,4.42,4.5],"y":[2,2.04,2.08,2.12,2.16,2.2,2.24,2.28,2.32,2.36,2.4,2.44,2.48,2.52,2.56,2.6,2.64,2.68,2.72,2.76,2.8,2.84,2.88,2.92,2.96,3,3.04,3.08,3.12,3.16,3.2,3.24,3.28,3.32,3.36,3.4,3.44,3.48,3.52,3.56,3.6,3.64,3.68,3.72,3.76,3.8,3.84,3.88,3.92,3.96,4],"z":[[6.24051390443049e-30,2.71358509223677e-26,1.16417581328961e-23,1.07727000537843e-21,3.44301695389835e-20,5.12788986411208e-19,4.34294653670383e-18,2.39905971894654e-17,9.52756127338737e-17,2.91991869845109e-16,7.27917912401602e-16,1.53618446087023e-15,2.83004078532567e-15,4.66173128177459e-15,6.99754181637247e-15,9.71800876074464e-15,1.26405911486134e-14,1.55545703892112e-14,1.82565903513485e-14,2.05783471300669e-14,2.24025926506172e-14,2.36676340024993e-14,2.43629367789094e-14,2.45192886362183e-14,2.41967276108584e-14,2.3472640016821e-14,2.24315091246195e-14,2.11569951847696e-14,1.97264485667927e-14,1.82076050056577e-14,1.66570428426826e-14,1.51199408690031e-14,1.36307106767541e-14,1.22141499805589e-14,1.08868467890345e-14,9.65864307263769e-15,8.53403312808196e-15,7.51342378567115e-15,6.59422152554065e-15,5.77173748758136e-15,5.0399177799219e-15,4.39191584404857e-15,3.82052801924289e-15,3.31851454139583e-15,2.87882727453111e-15,2.49476341210758e-15,2.16006181574703e-15,1.86895597877555e-15,1.61619504935002e-15,1.39704205114895e-15,1.20725645365537e-15],[9.02195780861847e-29,2.71401839309166e-25,8.8077988508857e-23,6.54881467830457e-21,1.75511380056356e-19,2.26166262073948e-18,1.69692347174977e-17,8.45763253205877e-17,3.07460238344689e-16,8.72596689703645e-16,2.03360775714741e-15,4.04354579913707e-15,7.06448512784474e-15,1.10967736657922e-14,1.59586084723749e-14,2.13195196145183e-14,2.67690325490692e-14,3.18938979511e-14,3.63420543922095e-14,3.98620024823742e-14,4.23163216789246e-14,4.36745399844857e-14,4.39931036676105e-14,4.33898652367367e-14,4.20187062259165e-14,4.00477411940978e-14,3.76426580576115e-14,3.49553954496748e-14,3.21175504371511e-14,2.92375410074009e-14,2.64004768441761e-14,2.36697930757321e-14,2.10898808686289e-14,1.86891449635941e-14,1.64830973985992e-14,1.447724354686e-14,1.26696277939982e-14,1.10529846523195e-14,9.61649259910132e-15,8.34715877760472e-15,7.23087873172242e-15,6.25322136384852e-15,5.39998900680736e-15,4.65759856763811e-15,4.01332398081324e-15,3.45543390360977e-15,2.97325242830859e-15,2.55716497776227e-15,2.19858667752974e-15,1.88990640665273e-15,1.62441638704523e-15],[1.18109632542843e-27,2.49189926448243e-24,6.18112870606517e-22,3.72290518232959e-20,8.42157667506544e-19,9.44006054196781e-18,6.30307277392452e-17,2.84530158388067e-16,9.49936234163803e-16,2.50376811679707e-15,5.4686058551398e-15,1.02675518605505e-14,1.70454889171111e-14,2.55772613945801e-14,3.52974499079045e-14,4.54257676739205e-14,5.51305562315473e-14,6.3675484476865e-14,7.05167168456133e-14,7.53425700062841e-14,7.80650436142538e-14,7.87802674651174e-14,7.7715039586213e-14,7.51727102900156e-14,7.1486593616564e-14,6.69845942427335e-14,6.19655276451781e-14,5.66857265113884e-14,5.13536962502229e-14,4.61304558069246e-14,4.11334664275346e-14,3.64424840571743e-14,3.21061283890426e-14,2.81483673916921e-14,2.45744398409121e-14,2.13759763484228e-14,1.8535241710956e-14,1.60285234125307e-14,1.38287484835331e-14,1.1907437354946e-14,1.023610973476e-14,8.78725195406544e-15,7.53494333321289e-15,6.45522463624221e-15,5.52627692452102e-15,4.72846539783087e-15,4.04429076346294e-15,3.45828051774732e-15,2.95684422530505e-15,2.52811027022954e-15,2.16175640211127e-15],[1.40014796943999e-26,2.10037350197944e-23,4.02364604115001e-21,1.97916677651035e-19,3.80367619979775e-18,3.72888995204353e-17,2.22563876388014e-16,9.13438978195528e-16,2.80994767486722e-15,6.897828466813e-15,1.41550271404293e-14,2.51510999775419e-14,3.97538813155296e-14,5.70846282484489e-14,7.57164832596962e-14,9.40051980040397e-14,1.10419678936525e-13,1.23780431872604e-13,1.33372871207849e-13,1.38948686059037e-13,1.40651501424853e-13,1.38906375544646e-13,1.34304650081797e-13,1.27503935052466e-13,1.1915229630033e-13,1.09838009587199e-13,1.00061751611189e-13,9.02261611080185e-14,8.06374496986045e-14,7.15144048736971e-14,6.30011562353448e-14,5.51811346402247e-14,4.80905710618121e-14,4.17305955643236e-14,3.60775068577247e-14,3.10911192651685e-14,2.67212959260078e-14,2.2912882720259e-14,1.96092986508318e-14,1.67550397440421e-14,1.4297332469255e-14,1.21871410563352e-14,1.03796983782776e-14,8.83469663278838e-15,7.51624416547345e-15,6.39266934742919e-15,5.4362315621565e-15,4.62278273830847e-15,3.9314099456031e-15,3.34407974741718e-15,2.84529768961484e-15],[1.50302651274563e-25,1.62521541466693e-22,2.42953597683867e-20,9.8392942924631e-19,1.6170955322712e-17,1.39393390372345e-16,7.47083806636045e-16,2.79835310733129e-15,7.95793334254372e-15,1.82460313833627e-14,3.52670748599139e-14,5.94336772972734e-14,8.96170693753946e-14,1.23365048498457e-13,1.57520227919548e-13,1.88940993197538e-13,2.15077506622324e-13,2.34286253301099e-13,2.45887088140014e-13,2.50035200469999e-13,2.47497722812455e-13,2.39410131415348e-13,2.27060993317303e-13,2.11728070655692e-13,1.94570106301406e-13,1.76567673875283e-13,1.58501774776882e-13,1.40958252550922e-13,1.24347667388579e-13,1.08932681188987e-13,9.48574401319638e-14,8.21755127524063e-14,7.08745174531948e-14,6.08966705626855e-14,5.21551858352723e-14,4.45468572034097e-14,3.79613496708712e-14,3.22877822578095e-14,2.74191666459468e-14,2.32552035701698e-14,1.97038606783564e-14,1.6682075383699e-14,1.4115852280994e-14,1.19399607294028e-14,1.00973852825445e-14,8.53863932733557e-15,7.22101938180356e-15,6.10785252465892e-15,5.16777090040524e-15,4.37403380761926e-15,3.70390836931778e-15],[1.46104448043732e-24,1.15444617308185e-21,1.36075043989448e-19,4.57432113835369e-18,6.47127448851876e-17,4.93131362280986e-16,2.38394515590279e-15,8.18082739964116e-15,2.15774762079666e-14,4.63406569803465e-14,8.4577106441426e-14,1.35485793755597e-13,1.95273389746646e-13,2.58150465133895e-13,3.17819852523929e-13,3.68829161920671e-13,4.0741584322791e-13,4.31774210493786e-13,4.418722761149e-13,4.39016212753217e-13,4.25340866365543e-13,4.03346680907552e-13,3.75542872461904e-13,3.44211015134211e-13,3.11276046745402e-13,2.78259855266472e-13,2.46290827164858e-13,2.16146297060245e-13,1.8831039074747e-13,1.63035334422232e-13,1.40398979632805e-13,1.20354785069314e-13,1.02772869009674e-13,8.74722119384087e-14,7.4244889456736e-14,6.28735669651494e-14,5.31435593509199e-14,4.48506732625718e-14,3.7805888429273e-14,3.18377490342877e-14,2.67931557153533e-14,2.25370881712892e-14,1.89516533711395e-14,1.59347454954695e-14,1.3398518741347e-14,1.12678095573903e-14,9.47859703638181e-15,7.97655559396616e-15,6.71572966331576e-15,5.65734341474435e-15,4.76874744559303e-15],[1.28606916126239e-23,7.5280899116293e-21,7.06944329926949e-19,1.98870558325808e-17,2.43761981607836e-16,1.65097650938082e-15,7.23161817788661e-15,2.28225247028135e-14,5.60143474356555e-14,1.13003969023514e-13,1.95236429302143e-13,2.97947988673193e-13,4.11278985420438e-13,5.23072046359856e-13,6.21905654130923e-13,6.99276674500902e-13,7.50542416362071e-13,7.74785827987609e-13,7.74017162804788e-13,7.52129563441412e-13,7.13907729835068e-13,6.6424771175709e-13,6.07633935771427e-13,5.47851128244424e-13,4.87877932399744e-13,4.29903253828093e-13,3.75413965633961e-13,3.25315201250566e-13,2.80057178486073e-13,2.39753063582088e-13,2.04280152464675e-13,1.73361814248161e-13,1.46630741424613e-13,1.23675667413882e-13,1.0407435337444e-13,8.74157012889217e-14,7.33135918439449e-14,6.14146505409578e-14,5.14017201270052e-14,4.29944196128307e-14,3.59478264686592e-14,3.00500369933054e-14,2.51191380219903e-14,2.0999953853825e-14,1.75608066219057e-14,1.46904374454454e-14,1.22951716770568e-14,1.02963677365746e-14,8.62816004977834e-15,7.23548830994734e-15,6.07239447875205e-15],[1.02510724000948e-22,4.50655068459546e-20,3.40677562317225e-18,8.08528768154375e-17,8.64299233982736e-16,5.23090691866613e-15,2.08538865406491e-14,6.07577779376389e-14,1.39218259624393e-13,2.6458361752277e-13,4.33803987243057e-13,6.32080941764123e-13,8.372807385425e-13,1.02626125324332e-12,1.1802303594638e-12,1.28764920596375e-12,1.34464294033896e-12,1.353697776727e-12,1.32159149192254e-12,1.25729577360407e-12,1.17027014639485e-12,1.06929432870406e-12,9.61811630614464e-13,8.53673556444391e-13,7.49156467925466e-13,6.5113603028799e-13,5.61333150983467e-13,4.80573899397873e-13,4.09029768570722e-13,3.46422006796696e-13,2.9218510035231e-13,2.45591124423444e-13,2.05839996235012e-13,1.72121852071527e-13,1.4365771887407e-13,1.1972396991272e-13,9.96651263544689e-14,8.2898614200818e-14,6.89142230162335e-14,5.72702860976116e-14,4.75880197730107e-14,3.95450110275655e-14,3.28685078231232e-14,2.73289235171665e-14,2.27337952972241e-14,1.89223189899302e-14,1.57605046937261e-14,1.31369482260675e-14,1.09591838549829e-14,9.15056788265751e-15,7.64763577846276e-15],[7.39909097550891e-22,2.47657837113722e-19,1.52283703370107e-17,3.07398400257011e-16,2.8845913079549e-15,1.56845086414444e-14,5.71677126283525e-14,1.54351842931179e-13,3.31277091750991e-13,5.94798609381602e-13,9.27792532456122e-13,1.29357160403973e-12,1.64758112574104e-12,1.94967478333961e-12,2.17224022619324e-12,2.30287740782762e-12,2.34278868754488e-12,2.30290933919219e-12,2.19956441119147e-12,2.05076051663276e-12,1.8735670388186e-12,1.68259687049842e-12,1.48937319959458e-12,1.30230458485766e-12,1.12701521331553e-12,9.66837620318426e-13,8.23339663466178e-13,6.96811432818345e-13,5.86676789458484e-13,4.91819407512533e-13,4.10827615643759e-13,3.42169294502343e-13,2.8431035957333e-13,2.35789983646637e-13,1.95264052920238e-13,1.61526241926459e-13,1.33514001257697e-13,1.10304904650248e-13,9.11072802957001e-14,7.52478578262438e-14,6.21582614060576e-14,5.1361520705753e-14,4.24593041616978e-14,3.51202570524009e-14,2.90696124548889e-14,2.40801058687544e-14,1.99641411153019e-14,1.65671088684908e-14,1.37617374053564e-14,1.14433490492715e-14,9.52589919655722e-15],[4.836058253697e-21,1.24941939999883e-18,6.31415024837284e-17,1.09292125176791e-15,9.06205010394451e-15,4.45064209624534e-14,1.48979638437181e-13,3.74191137073962e-13,7.54718324096842e-13,1.2838511684998e-12,1.90999775114378e-12,2.55384062433561e-12,3.13374491694952e-12,3.58652810484168e-12,3.87746346945441e-12,4.00008119033574e-12,3.96966326017871e-12,3.81458278367785e-12,3.56836228882026e-12,3.2638119979935e-12,2.92948593657842e-12,2.58808483017938e-12,2.25622575071446e-12,1.94502318442968e-12,1.66105078204071e-12,1.40739554522491e-12,1.18463746452935e-12,9.91675583442025e-13,8.2637787241136e-13,6.86064160304039e-13,5.67846381729989e-13,4.68854991367748e-13,3.86379244168954e-13,3.17945211134496e-13,2.61350732182983e-13,2.146719915346e-13,1.76252492149019e-13,1.44682046729235e-13,1.18770971239881e-13,9.75228658710795e-14,8.01080780195584e-14,6.58390460033011e-14,5.41481202865102e-14,4.45680694832451e-14,3.6715238268112e-14,3.02751863977861e-14,2.49905680592631e-14,2.0650984398976e-14,1.708454250954e-14,1.41508699665726e-14,1.17353577141059e-14],[2.86225794764126e-20,5.78645750090506e-18,2.42844335288503e-16,3.63376870689193e-15,2.67972750340716e-14,1.19517707071008e-13,3.69075576614271e-13,8.65659132052326e-13,1.64617752954161e-12,2.66070765261861e-12,3.78476996949203e-12,4.86387772446242e-12,5.76131477010023e-12,6.38842975193437e-12,6.712532032575e-12,6.74825563291131e-12,6.54136864202343e-12,6.15222663566971e-12,5.64279151335518e-12,5.06836656550584e-12,4.47355382007371e-12,3.89128065049229e-12,3.34369822868715e-12,2.84399263608202e-12,2.39845695081239e-12,2.00844351068048e-12,1.67201422638686e-12,1.38523430468135e-12,1.14312634981912e-12,9.40335179398547e-13,7.71563665037436e-13,6.31837205922135e-13,5.16646007001174e-13,4.2200424317391e-13,3.44455585505056e-13,2.81046381699362e-13,2.29281274386156e-13,1.87071113569997e-13,1.52679433693525e-13,1.24671244838867e-13,1.01866173834945e-13,8.32968671863232e-14,6.8172861842494e-14,5.58497116246481e-14,4.58029312197954e-14,3.76062181140255e-14,3.09133885222748e-14,2.54434843655739e-14,2.0968553609463e-14,1.73036623621665e-14,1.42987557764349e-14],[1.53401676608251e-19,2.46017297747368e-17,8.66348496584951e-16,1.12981368826929e-14,7.45893485891431e-14,3.0373837262516e-13,8.69192536949772e-13,1.91105010379765e-12,3.4376901441644e-12,5.29440766445957e-12,7.21889578691249e-12,8.93628571244751e-12,1.02381312170236e-11,1.1018483615217e-11,1.12699975250331e-11,1.10570424706291e-11,1.04828166261427e-11,9.66123586376906e-12,8.69784921853672e-12,7.67968833919301e-12,6.67195309936358e-12,5.71902794706215e-12,4.84771528804666e-12,4.0712111274222e-12,3.39294509614437e-12,2.80985486710214e-12,2.31495499799237e-12,1.89922369898278e-12,1.55290745328775e-12,1.26636680146734e-12,1.03058150106868e-12,8.37415491202471e-13,6.79720785257247e-13,5.51339288367932e-13,4.47044576300161e-13,3.62452356877391e-13,2.9391839863831e-13,2.38435593132187e-13,1.93536899828846e-13,1.57207645317308e-13,1.27808549002253e-13,1.04009567151098e-13,8.47339192716133e-14,6.9111293817831e-14,5.64390903592114e-14,4.61505516612926e-14,3.77887114311121e-14,3.09851931178136e-14,2.54430181794608e-14,2.09227045067387e-14,1.72310495087673e-14],[7.44484281089981e-19,9.60211434688607e-17,2.86687566438409e-15,3.28501627531309e-14,1.95427196144709e-13,7.30507869132203e-13,1.94593783124906e-12,4.02595552321604e-12,6.87313815922689e-12,1.01152201691886e-11,1.32533816875326e-11,1.58386069943825e-11,1.75857504437442e-11,1.84016750863928e-11,1.83510138653944e-11,1.7595886904861e-11,1.63373555335127e-11,1.47723001083133e-11,1.30684039899334e-11,1.13540778972611e-11,9.71834633306169e-12,8.2161337418094e-12,6.87563228344512e-12,5.70571735878482e-12,4.70237892805632e-12,3.85379823798158e-12,3.1440773135593e-12,2.55580825585799e-12,2.07172781048991e-12,1.67569599087575e-12,1.35320186767383e-12,1.09155576544199e-12,8.79885596268543e-13,7.09020282439712e-13,5.71316171906597e-13,4.60462401873437e-13,3.71287068932113e-13,2.99576476668762e-13,2.41913456441736e-13,1.95536823574095e-13,1.58221698767774e-13,1.28179151686521e-13,1.03973027945571e-13,8.4451639981325e-14,6.8692061659451e-14,5.59549528461421e-14,4.56480826579702e-14,3.72969762070688e-14,3.05213553740959e-14,2.50162672442381e-14,2.05369893374973e-14],[3.27178719865922e-18,3.44045955242132e-16,8.79987845118488e-15,8.9320132961477e-14,4.81964659045446e-13,1.66267728325256e-12,4.14146718655768e-12,8.09352313476324e-12,1.31565404052742e-11,1.85554308736582e-11,2.34211000167462e-11,2.70808604755232e-11,2.91972700716858e-11,2.97577922614684e-11,2.89797810035296e-11,2.71961907440888e-11,2.47616704308399e-11,2.19927044081661e-11,1.91392993512577e-11,1.63792057668048e-11,1.38251810765464e-11,1.15379432438926e-11,9.54011666116991e-12,7.82867665983637e-12,6.38490293692576e-12,5.18173116042884e-12,4.18882252600379e-12,3.37582310679825e-12,2.7142859609224e-12,2.17866183513898e-12,1.74667661215629e-12,1.39932955785638e-12,1.12067594722025e-12,8.97503127080599e-13,7.18969212208878e-13,5.76245753007813e-13,4.62187015724129e-13,3.71036469029085e-13,2.9817366287309e-13,2.39900401783076e-13,1.93262863545468e-13,1.55905336094066e-13,1.25951028221933e-13,1.01905618160975e-13,8.25796254649455e-14,6.70261960749482e-14,5.44914024155571e-14,4.43746391390154e-14,3.61971215681889e-14,2.95768617298759e-14,2.4208807135453e-14],[1.30202299711725e-17,1.13165590224387e-15,2.50550960596776e-14,2.27113179909248e-13,1.11883847566525e-12,3.58136723068402e-12,8.37899206103662e-12,1.55266582034543e-11,2.41116326763391e-11,3.26816886817117e-11,3.98393754825171e-11,4.46676882493017e-11,4.68559464787319e-11,4.65963478297301e-11,4.43842543645127e-11,4.08253322061489e-11,3.64982906246815e-11,3.18804343855909e-11,2.73226189534289e-11,2.30550731105266e-11,1.92082745020799e-11,1.58381668384104e-11,1.29497157476133e-11,1.05161780407305e-11,8.49350335735031e-12,6.83032861089118e-12,5.47442844115809e-12,4.3765345305915e-12,3.49232206317413e-12,2.78319286237053e-12,2.21631809582593e-12,1.76426261031563e-12,1.40440406564676e-12,1.11828081906815e-12,8.90947590571669e-13,7.10381458248496e-13,5.66957523340849e-13,4.5299953406596e-13,3.6240279723343e-13,2.9032265105675e-13,2.32920120202664e-13,1.87156127037901e-13,1.50626148355748e-13,1.21428084390918e-13,9.80571076188173e-14,7.93222477792088e-14,6.42803772087881e-14,5.21840569843494e-14,4.24403826129312e-14,3.45785335626811e-14,2.82241953268618e-14],[4.69198215051937e-17,3.41712355948322e-15,6.61709019092253e-14,5.40028222485287e-13,2.44479021051677e-12,7.30041545178819e-12,1.61154198278956e-11,2.84243219522358e-11,4.23067650785262e-11,5.52682451959122e-11,6.52292529948163e-11,7.10738813571819e-11,7.26822410274108e-11,7.0649789266635e-11,6.59267323630087e-11,5.95218071790699e-11,5.2319010098897e-11,4.49971389825055e-11,3.80199395805383e-11,3.16645167358705e-11,2.60642329110589e-11,2.12518648632551e-11,1.71961922673546e-11,1.38298979783033e-11,1.10691765004505e-11,8.82651243872312e-12,7.01832839802021e-12,5.56903955145368e-12,4.41274425069186e-12,3.49345907087654e-12,2.76453027508479e-12,2.18763868922478e-12,1.73165866284334e-12,1.37152388516874e-12,1.08718164242144e-12,8.62672221479485e-13,6.85343297738526e-13,5.45194140548728e-13,4.34336981660842e-13,3.46559966357707e-13,2.76975802512485e-13,2.21741306385988e-13,1.77834759869756e-13,1.42879899376045e-13,1.15007208145186e-13,9.27448607403342e-14,7.49331232909552e-14,6.06572392238036e-14,4.91948429116773e-14,3.99747677102388e-14,3.25447779727504e-14],[1.53108089539621e-16,9.47229741967893e-15,1.6210246516333e-13,1.20080287232337e-12,5.02849252615985e-12,1.40832900403472e-11,2.94648177884104e-11,4.96562564175328e-11,7.10708163739777e-11,8.97396981544455e-11,1.02800905048279e-10,1.09096829459399e-10,1.08976543983815e-10,1.03723624548046e-10,9.49714275521703e-11,8.4284404402224e-11,7.29358282218038e-11,6.18387425949414e-11,5.15695481345447e-11,4.24337995182718e-11,3.45414537035106e-11,2.78743529446589e-11,2.23393151813106e-11,1.78062101561729e-11,1.41331721327038e-11,1.11819486824451e-11,8.82625900225545e-12,6.95551850204941e-12,5.47569198791954e-12,4.30850794508218e-12,3.38984842186832e-12,2.66782355767735e-12,2.10082891515046e-12,1.65574506240237e-12,1.30635181153791e-12,1.03197773344208e-12,8.16376853388551e-13,6.46810216815244e-13,5.13304514472554e-13,4.08059403967472e-13,3.24977191827601e-13,2.59291713102553e-13,2.07276736855106e-13,1.66017589373114e-13,1.33232708002165e-13,1.07134437977458e-13,8.63205581561195e-14,6.96898026073621e-14,5.63760831598975e-14,4.56972665877181e-14,3.71152698617939e-14],[4.52422310791369e-16,2.41045108401283e-14,3.6835262405127e-13,2.49694008187384e-12,9.73544989917916e-12,2.57109722224615e-11,5.1212760534789e-11,8.27807919627741e-11,1.14306538756029e-10,1.39904368329129e-10,1.55946675669689e-10,1.61547322998811e-10,1.57935179680105e-10,1.47452560890897e-10,1.32685411232624e-10,1.15915915107444e-10,9.88818827251083e-11,8.27468513470087e-11,6.81817331129114e-11,5.54860324736554e-11,4.47069810093474e-11,3.5737828538482e-11,2.8390492437469e-11,2.24447868501216e-11,1.76790885364184e-11,1.38875830798281e-11,1.08884918082877e-11,8.5266410988982e-12,6.67275295874669e-12,5.22103997040868e-12,4.08609894014268e-12,3.19968889147702e-12,2.50770974338964e-12,1.96752906171246e-12,1.54570382519676e-12,1.21608842986194e-12,9.58292437489734e-13,7.56440599680352e-13,5.98186167019461e-13,4.73931871070015e-13,3.76218512630161e-13,2.99247241048922e-13,2.38507533555982e-13,1.90488186471407e-13,1.52453170864113e-13,1.22267980520456e-13,9.8265174962037e-14,7.91402874986011e-14,6.38712261536134e-14,5.16558360200867e-14,4.18634964345835e-14],[1.21058135216208e-15,5.63105374905442e-14,7.76407103034753e-13,4.85540728455288e-12,1.77417415886898e-11,4.44212425605315e-11,8.46184184150228e-11,1.31691249854509e-10,1.76014776969466e-10,2.09418809947494e-10,2.27708873300244e-10,2.30766594911054e-10,2.21241122638107e-10,2.02971366740632e-10,1.79784471053868e-10,1.54833041987411e-10,1.30372784732759e-10,1.07809586921485e-10,8.78689735983153e-11,7.07926417003026e-11,5.65131018390519e-11,4.47885645664933e-11,3.52973012960441e-11,2.76981618243828e-11,2.16658623424535e-11,1.69089509088043e-11,1.31767064073656e-11,1.02594887869916e-11,7.98558736122046e-12,6.21650116125184e-12,4.84180337009639e-12,3.77422290994504e-12,2.94524910749564e-12,2.3013699452632e-12,1.80094520797997e-12,1.41166063038719e-12,1.10848623470412e-12,8.72057369571162e-13,6.87401783822677e-13,5.42945159683916e-13,4.29737913679424e-13,3.40856166933078e-13,2.70938840522971e-13,2.1583057448556e-13,1.72306587077825e-13,1.37860796631936e-13,1.10542685359215e-13,8.88316660511358e-14,7.15402809421601e-14,5.77395591042546e-14,4.67014041421299e-14],[2.93324295210437e-15,1.20761743987116e-13,1.51798267581982e-12,8.82926093914015e-12,3.04339609275169e-11,7.26307842717437e-11,1.32911913958437e-10,1.99919889258764e-10,2.5949289430807e-10,3.00980141101713e-10,3.2004307723966e-10,3.18003322726048e-10,2.99566989457971e-10,2.7053599351073e-10,2.36254436022626e-10,2.00867168219373e-10,1.67167391047624e-10,1.36766069142697e-10,1.10381394688705e-10,8.813030261575e-11,6.9768922459785e-11,5.48683302459621e-11,4.29314528029424e-11,3.34640024472605e-11,2.6012852268753e-11,2.0183081526885e-11,1.56420651214969e-11,1.21163755011038e-11,9.38522019924966e-12,7.27267032901723e-12,5.63994786048631e-12,4.37841055518724e-12,3.40349395355589e-12,2.64965489183078e-12,2.06624971595396e-12,1.61423130709054e-12,1.26353539816033e-12,9.91031708668698e-13,7.78929139318018e-13,6.13540933231991e-13,4.84332272526652e-13,3.831877699983e-13,3.03849175871127e-13,2.41484278661579e-13,1.9235660845713e-13,1.53572420586753e-13,1.22886839838329e-13,9.85552549760815e-14,7.92193113024525e-14,6.38193576915965e-14,5.15271289571751e-14],[6.43585397801112e-15,2.37748307119776e-13,2.75293345562748e-12,1.50142685846378e-11,4.91408556379192e-11,1.1238506281422e-10,1.98461016293577e-10,2.8961885095412e-10,3.66268943328388e-10,4.15334241652623e-10,4.32973753546844e-10,4.22742502198196e-10,3.92069612129959e-10,3.49158929617305e-10,3.01097091274835e-10,2.53092339316325e-10,2.08454173360293e-10,1.68932973181921e-10,1.35160256592667e-10,1.07052077423011e-10,8.41228456243695e-11,6.57040228610528e-11,5.10828565650733e-11,3.95818684062611e-11,3.05981983755721e-11,2.36177816789242e-11,1.82150089616943e-11,1.40449110237706e-11,1.08322294557064e-11,8.35989196123565e-12,6.4582179962661e-12,4.99544935442855e-12,3.86977859781066e-12,3.00282333017446e-12,2.33438886098712e-12,1.81832514990913e-12,1.41928426360793e-12,1.11020278186105e-12,8.70358658216431e-13,6.83878020006287e-13,5.38591349839189e-13,4.25159224179513e-13,3.36405033855343e-13,2.66806086996046e-13,2.1210560944878e-13,1.69016878518657e-13,1.34997500779862e-13,1.08077069139911e-13,8.67254410448289e-14,6.97519400852975e-14,5.62281139700827e-14],[1.2786992720743e-14,4.29688611852286e-13,4.63101508359958e-12,2.38761968502563e-11,7.46876776465282e-11,1.64571368042885e-10,2.81707753812881e-10,4.00377248206227e-10,4.94963308598539e-10,5.50294757092439e-10,5.63818541412612e-10,5.42132832020115e-10,4.95990705089663e-10,4.36344066024761e-10,3.72161926821081e-10,3.09723226837329e-10,2.52792410679156e-10,2.03172799307114e-10,1.61322500407412e-10,1.26881303942602e-10,9.90615145748012e-11,7.69091116287783e-11,5.94621039208249e-11,4.58359429395823e-11,3.52614058793244e-11,2.70939017068085e-11,2.0807158158563e-11,1.59795492766877e-11,1.22779827285548e-11,9.44205029749714e-12,7.26975847718616e-12,5.60533768486885e-12,4.3291779522337e-12,3.34971489556781e-12,2.59699842406511e-12,2.01765841022549e-12,1.57100015244283e-12,1.22599680825948e-12,9.58984447891379e-13,7.51902060433223e-13,5.90951130926417e-13,4.65576504230486e-13,3.67692301605723e-13,2.91094219044736e-13,2.31013313540568e-13,1.83777070762657e-13,1.46551769871193e-13,1.17146448431878e-13,9.38635563938116e-14,7.53850194714398e-14,6.06851813036553e-14],[2.30056624834039e-14,7.12916403348947e-13,7.22617143591043e-12,3.55064508245953e-11,1.06850658548392e-10,2.28064554900006e-10,3.80132219537065e-10,5.28182119586505e-10,6.40389498822189e-10,7.00052731706357e-10,7.06710895242123e-10,6.70688785820933e-10,6.06491920021092e-10,5.28010813024858e-10,4.46124543176001e-10,3.68123279984641e-10,2.98134253215809e-10,2.37920454604104e-10,1.8768678216461e-10,1.46734711460497e-10,1.13929198303703e-10,8.79993057304232e-11,6.77128158963393e-11,5.19645920057262e-11,3.9810650857793e-11,3.04708673194457e-11,2.33154728100782e-11,1.78447029720542e-11,1.36669614092609e-11,1.04783001703832e-11,8.04446071801076e-12,6.18583233680595e-12,4.7652198503349e-12,3.67809973621408e-12,2.84497371624391e-12,2.20543394657674e-12,1.71359399750298e-12,1.33459236262106e-12,1.04192841335976e-12,8.15438909562961e-13,6.39764283112496e-13,5.03187665833504e-13,3.96756651823076e-13,3.1361902751086e-13,2.48520189946125e-13,1.974226488036e-13,1.57217683795133e-13,1.25506578060385e-13,1.00434408596837e-13,8.05635709908738e-14,6.4777376750066e-14],[3.74804813657974e-14,1.08585472291742e-12,1.04590420525165e-11,4.93776613768576e-11,1.43888954439476e-10,2.99101875327194e-10,4.87621507579595e-10,6.64920526872419e-10,7.93256578476501e-10,8.55074344094207e-10,8.52646217688055e-10,8.00427350830881e-10,7.16832401427236e-10,6.18677582842924e-10,5.18655615229464e-10,4.24949696045979e-10,3.41943322732615e-10,2.71277063465797e-10,2.12845875570102e-10,1.65577296449727e-10,1.27968826680851e-10,9.84229354559093e-11,7.54339734215585e-11,5.76766922565071e-11,4.40346773304004e-11,3.35953290620026e-11,2.56285340234672e-11,1.9559303542963e-11,1.49400723615031e-11,1.14254744259198e-11,8.75071538536893e-12,6.7137265826986e-12,5.16081903978076e-12,3.97536264450951e-12,3.06897195184004e-12,2.37471111366064e-12,1.8418934463513e-12,1.43212259974393e-12,1.11629044066197e-12,8.72306507184816e-13,6.83383740152796e-13,5.36745487479123e-13,4.22650633652339e-13,3.33658507479059e-13,2.64074311691159e-13,2.09530391876091e-13,1.66669720327962e-13,1.32906323783585e-13,1.06243674209685e-13,8.5136788133448e-14,6.83873263647052e-14],[5.52942110583062e-14,1.51828462905065e-12,1.4041940903612e-11,6.42147672780806e-11,1.82389451194648e-10,3.71225931759843e-10,5.94625206254183e-10,7.98780632289272e-10,9.40765642316234e-10,1.00280095533674e-09,9.90194712524768e-10,9.21527575383168e-10,8.18938639182726e-10,7.01929936773609e-10,5.84791222295599e-10,4.76438112327361e-10,3.81408868026442e-10,3.01168432234912e-10,2.35282483806808e-10,1.82306186871607e-10,1.4038231621831e-10,1.07604144382528e-10,8.22107482080198e-11,6.26736000583669e-11,4.77184408588623e-11,3.63123035746562e-11,2.7634485435733e-11,2.10424699085498e-11,1.60387019411604e-11,1.22409896531281e-11,9.35750036855927e-12,7.16635468983668e-12,5.49936448492719e-12,4.22929128399822e-12,3.25998550226804e-12,2.51882404865399e-12,1.95094909802232e-12,1.51490021964793e-12,1.17931422488952e-12,9.20437534028136e-13,7.20253737439238e-13,5.65075267822032e-13,4.44484335745227e-13,3.5053628336134e-13,2.77159933373766e-13,2.1970577733351e-13,1.74605132833447e-13,1.39112641413406e-13,1.11111412778369e-13,8.89653133767209e-14,7.14067815723031e-14],[7.38683267909177e-14,1.94887066883001e-12,1.74869454810354e-11,7.80945003713374e-11,2.17617582963142e-10,4.3602892856694e-10,6.8931236354379e-10,9.15708093125579e-10,1.0681875184131e-09,1.12918043311408e-09,1.10687094113244e-09,1.02348219162476e-09,9.04328512950398e-10,7.71135987997637e-10,6.39471803262742e-10,5.18800277800511e-10,4.13734610429131e-10,3.25552398019493e-10,2.53516809209807e-10,1.95855027096548e-10,1.50404104578909e-10,1.14994561193692e-10,8.76507675999542e-11,6.66745986705611e-11,5.06609767050678e-11,3.84777368074911e-11,2.92298831459214e-11,2.22197571492985e-11,1.69091398157515e-11,1.28859873400072e-11,9.83661826258097e-12,7.52319104492561e-12,5.76586623551823e-12,4.42890164911986e-12,3.409938187713e-12,2.63181400783525e-12,2.03634913089876e-12,1.57964728809388e-12,1.22855576852992e-12,9.58003408934174e-13,7.49001397640178e-13,5.87142719369765e-13,4.61475899145305e-13,3.63659325094355e-13,2.87325752135164e-13,2.27604230643644e-13,1.80759983502653e-13,1.43922714942544e-13,1.14881286749201e-13,9.1928264419295e-14,7.37419909110239e-14],[8.93595447832514e-14,2.29647222353877e-12,2.02000458148305e-11,8.8815165703859e-11,2.44405094467468e-10,4.84674453428105e-10,7.5962825781998e-10,1.00174762043783e-09,1.16121285489678e-09,1.22081453288572e-09,1.19096231358003e-09,1.09657359819478e-09,9.65255338926858e-10,8.20306210323305e-10,6.7817339313698e-10,5.48679377186893e-10,4.36462892353487e-10,3.42647389290404e-10,2.66266623291266e-10,2.05305571204487e-10,1.57378732133191e-10,1.20127162591851e-10,9.14215022501397e-11,6.94428682989227e-11,5.26934650314152e-11,3.99710960152287e-11,3.03284947047727e-11,2.30293227453876e-11,1.75069139275734e-11,1.33283918091729e-11,1.01648612101325e-11,7.76738843999116e-12,5.94805267081102e-12,4.56522376060821e-12,3.51225009521017e-12,2.70883700608557e-12,2.09451466822881e-12,1.62371009667086e-12,1.26204029332399e-12,9.83529328474929e-13,7.6852139787535e-13,6.02116520354753e-13,4.72997904969664e-13,3.72552476817117e-13,2.94210703437697e-13,2.32950466622927e-13,1.84923696648535e-13,1.47174945444337e-13,1.17428887474377e-13,9.39295638701732e-14,7.53185280059533e-14],[9.78876096812134e-14,2.48420669451568e-12,2.16442397634631e-11,9.44571748415632e-11,2.583738354796e-10,5.0985042126981e-10,7.95789943385773e-10,1.04575831632351e-09,1.20857736409834e-09,1.26728349609615e-09,1.23345611406507e-09,1.13339376728913e-09,9.95862381866844e-10,8.44945794683494e-10,6.97523570513796e-10,5.63588089402819e-10,4.47782593287006e-10,3.51147057560015e-10,2.72596018323239e-10,2.09990400336033e-10,1.6083163059546e-10,1.22665025905861e-10,9.32838559530931e-11,7.0808658019212e-11,5.36952469262323e-11,4.07064671269487e-11,3.08690106989911e-11,2.34273027281167e-11,1.78005516167818e-11,1.35455512228988e-11,1.03258725273991e-11,7.88709552528973e-12,6.03730661816161e-12,4.6319695497037e-12,3.56231605188254e-12,2.74650801128866e-12,2.12294839836548e-12,1.64523948412642e-12,1.27839355777533e-12,9.95990283581534e-13,7.78046455089335e-13,6.09420261490983e-13,4.7861580712277e-13,3.76887000009885e-13,2.97565239234542e-13,2.35554410484906e-13,1.86951014718474e-13,1.48757961604976e-13,1.18668549740385e-13,9.49031107221402e-14,7.60852294068204e-14],[9.7099856802994e-14,2.46696286504126e-12,2.15121541473729e-11,9.39428897696274e-11,2.57103989857156e-10,5.07566865917196e-10,7.92516060375736e-10,1.04178014242467e-09,1.20430187355758e-09,1.26309381731776e-09,1.22962882419386e-09,1.1300805353361e-09,9.93110489800736e-10,8.4273206671053e-10,6.9578621731693e-10,5.62250315858671e-10,4.46767420173264e-10,3.50385171229017e-10,2.72028929205242e-10,2.09570835086397e-10,1.60522515546852e-10,1.22437909992618e-10,9.3117248051394e-11,7.06865114375e-11,5.36056808230373e-11,4.06407379487743e-11,3.08207105264306e-11,2.339174806616e-11,1.77743246282806e-11,1.35261592416153e-11,1.03114973917984e-11,7.87641009182008e-12,6.02934097570022e-12,4.62601371888131e-12,3.55784932064991e-12,2.74314764376403e-12,2.12041240053693e-12,1.64331955514498e-12,1.276935417923e-12,9.94879345446007e-13,7.77197367706961e-13,6.08769264937298e-13,4.78115129544981e-13,3.76500741590482e-13,2.97266340829757e-13,2.35322415234045e-13,1.86770410724441e-13,1.48616951457826e-13,1.18558134392027e-13,9.48164054754371e-14,7.6016951756297e-14],[8.72194904748189e-14,2.24898132884529e-12,1.98324811212472e-11,8.73723507668065e-11,2.40819198374894e-10,4.78191191872571e-10,7.50291434045064e-10,9.90358796954906e-10,1.1489326020796e-09,1.20874636589486e-09,1.17991037000735e-09,1.0869848949885e-09,9.5727548602026e-10,8.13875568431668e-10,6.73118533903248e-10,5.44781488723955e-10,4.33501086991848e-10,3.40421891345307e-10,2.64608312209996e-10,2.04077413774203e-10,1.56473039140092e-10,1.19461146176014e-10,9.0932531569764e-11,6.9084116178929e-11,5.24302193689056e-11,3.97777831966741e-11,3.01863540304295e-11,2.29246298025769e-11,1.7429644841034e-11,1.32712304408471e-11,1.01224673310817e-11,7.73586142828377e-12,5.92454007919039e-12,4.54763636870058e-12,3.49905479144403e-12,2.69890633569838e-12,2.08701753542008e-12,1.61803231244661e-12,1.25772675530581e-12,9.80241880895321e-13,7.660080648212e-13,6.00188997250844e-13,4.71515055097607e-13,3.7140820199579e-13,2.9332500717864e-13,2.32262852336909e-13,1.84388277711854e-13,1.46756813309965e-13,1.17101406660878e-13,9.36723516186769e-14,7.51159410376485e-14],[7.09434968048495e-14,1.88216390754256e-12,1.69598411880012e-11,7.59915438540821e-11,2.12322198573957e-10,4.26351415150695e-10,6.75249381777955e-10,8.98422857726854e-10,1.04942650629991e-09,1.11063791468997e-09,1.08980463605792e-09,1.00860975293995e-09,8.91902605746064e-10,7.61087037417414e-10,6.31547570885814e-10,5.12672129632745e-10,4.09065914700919e-10,3.2203592354661e-10,2.50890767489871e-10,1.93906217817239e-10,1.48964282041963e-10,1.13933926298014e-10,8.68708234465518e-11,6.61015031245179e-11,5.0239859918796e-11,3.81680863009953e-11,2.90019203420852e-11,2.20516580621215e-11,1.67849383495068e-11,1.27940123556532e-11,9.76833853034321e-12,7.47236686555962e-12,5.72792896123975e-12,4.40050115748617e-12,3.38861339713314e-12,2.61575316308125e-12,2.02421540728261e-12,1.57045184708095e-12,1.22156525998423e-12,9.52672478697354e-13,7.44923356577532e-13,5.84013416212481e-13,4.59067205830382e-13,3.61799631703605e-13,2.85885583074272e-13,2.26485610271748e-13,1.79888553073168e-13,1.43241873247101e-13,1.14347822981576e-13,9.15090941838058e-14,7.34117098893119e-14],[5.22535410875352e-14,1.44603027504622e-12,1.34529675977747e-11,6.18069989431578e-11,1.76206410759212e-10,3.59742437644506e-10,5.77711074764216e-10,7.77751329975869e-10,9.17714916277327e-10,9.79822822131309e-10,9.68886565498512e-10,9.02834938719829e-10,8.03228398185397e-10,6.89157457716273e-10,5.74671133596748e-10,4.68577906064225e-10,3.75397005160836e-10,2.96623966977741e-10,2.31877539908461e-10,1.79771658259172e-10,1.38504488188841e-10,1.06217253510634e-10,8.11884221037852e-11,6.19207113562764e-11,4.71640456626997e-11,3.59038493253555e-11,2.73332283095205e-11,2.08199380537868e-11,1.58740135256126e-11,1.21188447657898e-11,9.26669119987311e-12,7.09866747617733e-12,5.44877392675648e-12,4.19137136556127e-12,3.23147940519488e-12,2.4973305051502e-12,1.93469370963121e-12,1.50256866043548e-12,1.16993047565461e-12,9.13274877028006e-13,7.14769593650197e-13,5.60863401116245e-13,4.41239722748823e-13,3.48029234677127e-13,2.75216984433885e-13,2.18195542839918e-13,1.73427808492974e-13,1.38192191937863e-13,1.10389743130375e-13,8.83979078961962e-14,7.09594323344385e-14],[3.48516185884104e-14,1.0198720355322e-12,9.89842266738581e-12,4.7010101373152e-11,1.37648034142656e-10,2.87258881559075e-10,4.69861089862274e-10,6.4249902460038e-10,7.68354850120482e-10,8.29966089177304e-10,8.29128544734194e-10,7.79613034232542e-10,6.99200617406015e-10,6.04241314720114e-10,5.07144230672275e-10,4.15957192621991e-10,3.35029246763397e-10,2.66025479656939e-10,2.0889377335809e-10,1.62623539433745e-10,1.25772187599618e-10,9.67949473942348e-11,7.42300529572672e-11,5.67874033709111e-11,4.33780044406128e-11,3.31102498402137e-11,2.52698801413777e-11,1.92937604233695e-11,1.47431242091158e-11,1.12791029419189e-11,8.64168338602188e-12,6.6323070246019e-12,5.09985865657341e-12,3.92959451134843e-12,3.03451193425555e-12,2.34868947602958e-12,1.82218546653498e-12,1.41715154767356e-12,1.10488338277834e-12,8.635886560232e-13,6.76700933344881e-13,5.31607208496376e-13,4.18688049300977e-13,3.30593498512428e-13,2.61696564427074e-13,2.07680411925005e-13,1.6522620606095e-13,1.31776756452929e-13,1.05357286868846e-13,8.4439298001322e-14,6.78369777214711e-14],[2.10491357138025e-14,6.60331986835252e-13,6.75562409559512e-12,3.34368887693402e-11,1.01213939200904e-10,2.17076637140693e-10,3.6327922396448e-10,5.06495887544727e-10,6.15905622175295e-10,6.75011058061252e-10,6.82960285544264e-10,6.49434513795699e-10,5.88309252022219e-10,5.12991529910565e-10,4.34052627147462e-10,3.58624703213401e-10,2.90783021909707e-10,2.32303262444056e-10,1.83436228376046e-10,1.4354176736276e-10,1.1154354732886e-10,8.62235551623186e-11,6.63943229261821e-11,5.0987011440726e-11,3.90862470708891e-11,2.99339977006723e-11,2.29173034071814e-11,1.75490493365876e-11,1.34470830059928e-11,1.03144667329796e-11,7.92212482124836e-12,6.09426808309391e-12,4.69651458059707e-12,3.6264102111231e-12,2.80597886639531e-12,2.17593289691757e-12,1.69121103095907e-12,1.3175603951052e-12,1.028930016302e-12,8.05489480531679e-13,6.32126082037858e-13,4.97306463821465e-13,3.92214960333044e-13,3.10101499491397e-13,2.45787969994775e-13,1.95294314198319e-13,1.55555048993775e-13,1.24204095482242e-13,9.94112345515486e-14,7.97576112780479e-14,6.41408062817134e-14],[1.15119706556463e-14,3.92488864918433e-13,4.27677636103546e-12,2.22403529495084e-11,7.00539532597808e-11,1.55242465940454e-10,2.67007789525879e-10,3.81022932188859e-10,4.72677342330252e-10,5.27107467077637e-10,5.41494042560858e-10,5.2188784115837e-10,4.78465557380676e-10,4.21713781330526e-10,3.60289895488015e-10,3.00300805858695e-10,2.45442506564666e-10,1.97516081502767e-10,1.57013695899052e-10,1.2362487482236e-10,9.66147329967671e-11,7.50783604841572e-11,5.80961869492593e-11,4.48186298126716e-11,3.45043828034631e-11,2.6530644611063e-11,2.03878733209225e-11,1.56671345593361e-11,1.20448786742915e-11,9.26782617717165e-12,7.13928438408977e-12,5.50741279780978e-12,4.25550783889241e-12,3.29415259612248e-12,2.55498309029657e-12,1.98580093620735e-12,1.54677766463746e-12,1.20752751507058e-12,9.44861685906468e-13,7.41071895638924e-13,5.82621990966009e-13,4.5915236931266e-13,3.62723232712757e-13,2.87239657349524e-13,2.28014799575248e-13,1.81437922098247e-13,1.44721908175275e-13,1.15711044475692e-13,9.27345116970093e-14,7.44945601006209e-14,5.99810279571612e-14],[5.70123797901234e-15,2.14161154039184e-13,2.51141907868064e-12,1.38337088673062e-11,4.56401407295554e-11,1.05066873249051e-10,1.86560455070929e-10,2.73525642441329e-10,3.47307119927671e-10,3.95207512355852e-10,4.13253524188323e-10,4.0458011393139e-10,3.76128990995025e-10,3.35685988618112e-10,2.9004178457245e-10,2.4422916562763e-10,2.01476740738348e-10,1.63517670364305e-10,1.31003460331988e-10,1.0388817953437e-10,8.17299688050967e-11,6.39027063902024e-11,4.97313007276497e-11,3.85699491011344e-11,2.98414856221637e-11,2.30521640321446e-11,1.7792149448737e-11,1.37285546533915e-11,1.05952828909114e-11,8.1821579938233e-12,6.32466247243938e-12,4.89488898807406e-12,3.79389493185001e-12,2.94542583336188e-12,2.29086635041908e-12,1.78523848601302e-12,1.39406443341497e-12,1.09092729149728e-12,8.55585956940698e-13,6.72524855845182e-13,5.29841857133109e-13,4.18397458804313e-13,3.31164839047501e-13,2.62733777240595e-13,2.08932144605651e-13,1.66537073563774e-13,1.33054459499001e-13,1.06550503372744e-13,8.55228854757329e-14,6.88021292025007e-14,5.5475977010802e-14],[2.55677643656031e-15,1.0727596012638e-13,1.3679600698131e-12,8.04667998817799e-12,2.79887374078987e-11,6.72943978057462e-11,1.23916045168689e-10,1.8737718889688e-10,2.44321042758004e-10,2.84504379414871e-10,3.03573668480517e-10,3.02564120273141e-10,2.85801210760961e-10,2.5873575971956e-10,2.2644766565882e-10,1.92913795747739e-10,1.60840147698781e-10,1.31808069438159e-10,1.06541990122972e-10,8.51842105275863e-11,6.75240336068148e-11,5.3166655335582e-11,4.16464046289922e-11,3.24960839855098e-11,2.52849735292128e-11,1.96361534971343e-11,1.52311602946126e-11,1.18075372828662e-11,9.15289471042119e-12,7.09768504599e-12,5.50794628020233e-12,4.27865438242782e-12,3.32795456559396e-12,2.59232867478369e-12,2.02264453100463e-12,1.58098258857877e-12,1.23811979633038e-12,9.71553778020453e-13,7.63962539618272e-13,6.02010218383574e-13,4.75424856362041e-13,3.76288312480827e-13,2.98490624613479e-13,2.37311287241708e-13,1.89098158759988e-13,1.51021296871563e-13,1.20884210075135e-13,9.69790649322007e-14,7.79755298190532e-14,6.28353580331451e-14,5.0746673628417e-14],[1.0382942065425e-15,4.93301544648127e-14,6.91161017850914e-13,4.37699419159986e-12,1.61562902357144e-11,4.07896371504708e-11,7.82434131245767e-11,1.22491832616082e-10,1.6455320483632e-10,1.96648420438052e-10,2.14652663487562e-10,2.18280961879767e-10,2.09909670226164e-10,1.93102332617549e-10,1.71464382913884e-10,1.47997295459418e-10,1.24870087792922e-10,1.03450926606207e-10,8.44601112305548e-11,6.815296664304e-11,5.44846907952615e-11,4.32389406786551e-11,3.41185618655937e-11,2.68042995942738e-11,2.09894207204297e-11,1.63976628789466e-11,1.27904445430706e-11,9.96765732653907e-12,7.76497674015281e-12,6.04956946410569e-12,4.71532584033003e-12,3.67824547556846e-12,2.87228587369203e-12,2.24579251459736e-12,1.75852061738701e-12,1.37920318063324e-12,1.0835959005281e-12,8.52923637991311e-13,6.72656722498341e-13,5.31553414266898e-13,4.20914349847779e-13,3.34004181074839e-13,2.65604114129851e-13,2.11666367348427e-13,1.69047654872625e-13,1.35303759259381e-13,1.08531225155392e-13,8.72453468440463e-14,7.02860855632687e-14,5.67454712004707e-14,4.59115300487068e-14],[3.81814305645555e-16,2.08243231229879e-14,3.23919157130659e-13,2.22646746083217e-12,8.77853391237408e-12,2.33979926738808e-11,4.69656481697215e-11,7.64133580940221e-11,1.0610848208287e-10,1.30505769133747e-10,1.4609424710619e-10,1.51914711048229e-10,1.49019106501248e-10,1.39548895946485e-10,1.25915381814552e-10,1.10272952877896e-10,9.42793930939206e-11,7.90572764804139e-11,6.52642422425431e-11,5.32038576584702e-11,4.2936799873218e-11,3.43737067752146e-11,2.73444647077364e-11,2.16455871398952e-11,1.70700301688125e-11,1.34241966841012e-11,1.05362573252505e-11,8.25897473949424e-12,6.46930511717483e-12,5.06630221751614e-12,3.9682899088457e-12,3.10987801866906e-12,2.43913658741641e-12,1.91507942369557e-12,1.50550933565125e-12,1.18522206940457e-12,9.34537869133901e-13,7.3811787660056e-13,5.8402026502113e-13,4.62953623254484e-13,3.67689991392009e-13,2.926055505548e-13,2.33322450561846e-13,1.86430212109211e-13,1.49269408798926e-13,1.19763900592284e-13,9.62908058000534e-14,7.75797452729243e-14,6.26347593000031e-14,5.0673770048552e-14,4.10816159273294e-14],[1.27141711065779e-16,8.07007676615793e-15,1.40813928603057e-13,1.05910221528373e-12,4.48977256808351e-12,1.27017975701526e-11,2.67994045493893e-11,4.54886638014234e-11,6.55076686703975e-11,8.31585102411397e-11,9.57094008550587e-11,1.01992760120019e-10,1.02256892453508e-10,9.76501941776577e-11,8.96772838489096e-11,7.98011154179987e-11,6.92260491811542e-11,5.8825332502694e-11,4.91577229471127e-11,4.05260406977283e-11,3.30463824104489e-11,2.67111943486456e-11,2.14394500982447e-11,1.71129842246089e-11,1.36007861119347e-11,1.07739629486587e-11,8.51403003674641e-12,6.71673851629504e-12,5.29310967634202e-12,4.16885317038307e-12,3.28295361813097e-12,2.5859203419115e-12,2.03799335576711e-12,1.6074650685623e-12,1.26919259581663e-12,1.00332475092338e-12,7.94239205331924e-13,6.29670814585127e-13,5.00006159360896e-13,3.97718313361542e-13,3.16917421110715e-13,2.52995443666101e-13,2.02346589402385e-13,1.62148041275686e-13,1.30188399311882e-13,1.04733689357383e-13,8.44228333122941e-14,6.81861578704246e-14,5.51818812340374e-14,4.47466083795367e-14,3.63567317051752e-14],[3.83378714960276e-17,2.87099734832084e-15,5.67814109373706e-14,4.71129764336468e-13,2.16146744682479e-12,6.52543700169164e-12,1.45372500179168e-11,2.58409701616425e-11,3.8719743417722e-11,5.08769926598152e-11,6.03532595559369e-11,6.60578443724334e-11,6.78241489069506e-11,6.61648967288614e-11,6.19419535464456e-11,5.60884775223434e-11,4.94329720528467e-11,4.26188778305523e-11,3.60911750417099e-11,3.01202051207587e-11,2.4840323334195e-11,2.02897111131996e-11,1.64446019026254e-11,1.32456599561508e-11,1.0616701807753e-11,8.47702505522988e-12,6.7488856024678e-12,5.36154567603015e-12,4.25304457119827e-12,3.37055165125356e-12,2.66990477525993e-12,2.11473558338861e-12,1.67543503022431e-12,1.32810952731192e-12,1.05360954238143e-12,8.36668924796461e-13,6.65166858779853e-13,5.29509397076453e-13,4.22119872739052e-13,3.37024301156219e-13,2.69517299464947e-13,2.15894869641732e-13,1.73241875381572e-13,1.39263753356148e-13,1.12153691824605e-13,9.04880592399482e-14,7.31442199274009e-14,5.92360218473417e-14,4.80631936456246e-14,3.90716657374079e-14,3.18224577209838e-14],[1.04682005151306e-17,9.37640310974035e-16,2.12382304067622e-14,1.9598568449464e-13,9.79478849056094e-13,3.17257460192964e-12,7.49638124667011e-12,1.40083243797717e-11,2.19114482157274e-11,2.98864207163446e-11,3.66329179552852e-11,4.12729004601289e-11,4.34827739294572e-11,4.34100202232623e-11,4.1494080359048e-11,3.82880346048015e-11,3.43287749284715e-11,3.00645500219567e-11,2.58287324059534e-11,2.18431048041642e-11,1.82360021165758e-11,1.50651700026733e-11,1.23395292976338e-11,1.00372080310257e-11,8.11916027092781e-12,6.53871297502811e-12,5.2477970948842e-12,4.20069204085737e-12,3.35602168264725e-12,2.67759109794304e-12,2.13450151741255e-12,1.70085051569728e-12,1.35522250133486e-12,1.0800996718055e-12,8.61271247906313e-13,6.8728373870462e-13,5.48952478307473e-13,4.3894089708735e-13,3.51406062621049e-13,2.81704880340411e-13,2.26153549257705e-13,1.81832465496855e-13,1.46429133493814e-13,1.18112390877617e-13,9.54321422661802e-14,7.72396943109793e-14,6.26246178325937e-14,5.08648003508136e-14,4.13869841831724e-14,3.37356146845153e-14,2.75482595781088e-14],[2.58833305277959e-18,2.81117642771532e-16,7.36855041737483e-15,7.62411256408218e-14,4.1779518586158e-13,1.45972791350336e-12,3.6747970765008e-12,7.24661695161551e-12,1.18715651414198e-11,1.68563725464522e-11,2.1402620267821e-11,2.48766056958833e-11,2.69458108669952e-11,2.75778343589309e-11,2.69579077237371e-11,2.53850035414674e-11,2.31843164279288e-11,2.06501154374477e-11,1.80176427082727e-11,1.54562277850456e-11,1.30749817808009e-11,1.09342204853953e-11,9.05814626656403e-12,7.44635473226197e-12,6.08314958169363e-12,4.94449450946114e-12,4.00285706365882e-12,3.23036013916738e-12,2.60067070060457e-12,2.09000057395304e-12,1.67751663042746e-12,1.34538122179117e-12,1.07857860387079e-12,8.64632129995524e-13,6.93279393451563e-13,5.56145995943502e-13,4.4644068182037e-13,3.5868291393744e-13,2.88466714575511e-13,2.3226033665987e-13,1.8723903659903e-13,1.51147168390208e-13,1.22185518647068e-13,9.89199302706054e-14,8.02076115809853e-14,6.51379700502309e-14,5.29852699650394e-14,4.31708498701796e-14,3.52330281359499e-14,2.88031658819149e-14,2.35866455381173e-14],[5.79525264283891e-19,7.737279548351e-17,2.37135936765886e-15,2.77354611516101e-14,1.677466310212e-13,6.35608666714062e-13,1.71248726158674e-12,3.57730658451637e-12,6.15804930932526e-12,9.12834568689588e-12,1.20361344117798e-11,1.44644789812127e-11,1.61401066237863e-11,1.6964386200771e-11,1.69857612078901e-11,1.6346173912621e-11,1.5227362730196e-11,1.38103707397735e-11,1.225139817849e-11,1.06714969601066e-11,9.15570138971643e-12,7.75741872723933e-12,6.50497409703955e-12,5.40836495145912e-12,4.46520871115637e-12,3.66549255762108e-12,2.99509918779079e-12,2.43826164176711e-12,1.97916387155067e-12,1.60290371878164e-12,1.2960055802007e-12,1.04663130390737e-12,8.44600204796018e-13,6.81297036507185e-13,5.49521542833832e-13,4.4331444001908e-13,3.57781302480022e-13,2.88926647955979e-13,2.33504456558584e-13,1.8888751703807e-13,1.52955682488629e-13,1.24001827665867e-13,1.00653668723505e-13,8.18093831829246e-14,6.65849851832193e-14,5.42715587426138e-14,4.43006604757664e-14,3.62164307659048e-14,2.96531745223263e-14,2.43173765913721e-14,1.99732970011795e-14],[1.174975143066e-19,1.95495528038201e-17,7.07887546613416e-16,9.4354501519483e-15,6.33966322596567e-14,2.61918114412202e-13,7.5863631483222e-13,1.68518955555167e-12,3.05827566759689e-12,4.74632832697778e-12,6.51526015560998e-12,8.11334617985755e-12,9.3446420102679e-12,1.01047125644515e-11,1.03796483273655e-11,1.02230323349732e-11,9.72634114407341e-12,8.99297257395136e-12,8.12018915571047e-12,7.18918858457179e-12,6.26154082311411e-12,5.37975203422221e-12,4.57001179020358e-12,3.84573832417691e-12,3.2110784601722e-12,2.66393487296396e-12,2.19836811190866e-12,1.80637924782128e-12,1.47915582143058e-12,1.20788989704024e-12,9.84275283022462e-13,8.00776317966152e-13,6.5074186647807e-13,5.28419971916862e-13,4.28913032212677e-13,3.48100989140085e-13,2.82550697777958e-13,2.29422905814185e-13,1.86383578696494e-13,1.51523150101133e-13,1.23285233730057e-13,1.00405069224979e-13,8.18572423477893e-14,6.68118366756577e-14,5.45980136711444e-14,4.46739929639158e-14,3.66024568792887e-14,3.00304949740057e-14,2.46733119691478e-14,2.03010318498057e-14,1.67280340961934e-14],[2.15719335809502e-20,4.53454503962987e-18,1.96012042191638e-16,3.00172567413114e-15,2.25528055491611e-14,1.02140760826818e-13,3.19486268525969e-13,7.57553128803433e-13,1.45414723464746e-12,2.36952457876349e-12,3.39469800135234e-12,4.39018436528794e-12,5.22949875628854e-12,5.82797391234514e-12,6.15147208805589e-12,6.20966377902334e-12,6.04183290673299e-12,5.701856438664e-12,5.24613477780403e-12,4.72571038744957e-12,4.18224896099827e-12,3.64689197806522e-12,3.14090337435643e-12,2.67722543805427e-12,2.26233001627466e-12,1.89799770172452e-12,1.58284249640115e-12,1.31352042139305e-12,1.08563011612741e-12,8.94347180718251e-13,7.34845362603313e-13,6.02556623084127e-13,4.93315202710999e-13,4.0342196588381e-13,3.29656656956161e-13,2.69258209561386e-13,2.1988722219883e-13,1.7958010474806e-13,1.46701017413359e-13,1.19895325085118e-13,9.80466451166148e-14,8.02384769169463e-14,6.57207088100861e-14,5.38808798873207e-14,4.4219842420682e-14,3.63313594766436e-14,2.9885137685668e-14,2.46128059914457e-14,2.0296387215278e-14,1.67588572468264e-14,1.38564384064254e-14],[3.58635733882035e-21,9.65559332635456e-19,5.03445911316874e-17,8.93018625420776e-16,7.55191283983295e-15,3.76955834121887e-14,1.27903684953062e-13,3.24974417683351e-13,6.61970169476188e-13,1.13580140206211e-12,1.70253158466183e-12,2.29166457061935e-12,2.82877618061681e-12,3.25476063960281e-12,3.53569072516059e-12,3.66337325068682e-12,3.64991146245054e-12,3.52001379833053e-12,3.30373761656008e-12,3.03100759581705e-12,2.72820886980082e-12,2.41656876450687e-12,2.11182213865949e-12,1.82465863943786e-12,1.56155355878271e-12,1.32571014359396e-12,1.11795176806116e-12,9.37484267025842e-13,7.82502296233497e-13,6.50644580920304e-13,5.39318113863214e-13,4.45916610836078e-13,3.67958157078811e-13,3.03163877466509e-13,2.49495402163944e-13,2.05164854494083e-13,1.68627525511532e-13,1.3856448510452e-13,1.13860113511076e-13,9.35778439701905e-14,7.69361839358998e-14,6.32862256726053e-14,5.20912760113735e-14,4.29088547827323e-14,3.53750734677459e-14,2.9191265817211e-14,2.41126682624959e-14,1.99389167907963e-14,1.65061224649734e-14,1.3680298943756e-14,1.13519348962592e-14],[5.39910949434682e-22,1.88743743845632e-19,1.19942878185841e-17,2.48445523445111e-16,2.38032012514556e-15,1.31655703405655e-14,4.86772693387031e-14,1.33032267249385e-13,2.88513900175177e-13,5.22734693394586e-13,8.21890310245595e-13,1.15399753778468e-12,1.47903426507859e-12,1.76006348530128e-12,1.97091672098029e-12,2.09903164577606e-12,2.14432375358689e-12,2.11586293745735e-12,2.02798369727712e-12,1.89687906032827e-12,1.7381386634236e-12,1.56527638347423e-12,1.38907471887578e-12,1.21750228475724e-12,1.05597514837452e-12,9.07783520178492e-13,7.74562580110439e-13,6.56735377800645e-13,5.53892062645962e-13,4.65093610203187e-13,3.89102236339393e-13,3.24547732558122e-13,2.7004152703087e-13,2.24250261772579e-13,1.85939359920257e-13,1.53995239700297e-13,1.27432970465861e-13,1.05394491149423e-13,8.71411137050805e-14,7.20429265168044e-14,5.95668690213823e-14,4.92646268458803e-14,4.07610517316801e-14,3.37435012879017e-14,2.79522854398628e-14,2.3172271460621e-14,1.9225616201289e-14,1.59655464671053e-14,1.32710846571874e-14,1.10426083928058e-14,9.19813402758501e-15],[7.36028786825893e-23,3.3869947082583e-20,2.65062138415159e-18,6.46372657377355e-17,7.0621310788399e-16,4.35157741448355e-15,1.76109039719739e-14,5.19680656495589e-14,1.20390813550535e-13,2.30992559390992e-13,3.81906625792135e-13,5.6058858950346e-13,7.47479026453336e-13,9.2160629424803e-13,1.06551868991481e-12,1.16810406378651e-12,1.22515994744897e-12,1.23835674694311e-12,1.21343404953501e-12,1.15831039959803e-12,1.08150938602523e-12,9.91056752233441e-13,8.93839170534089e-13,7.95333753805233e-13,6.995945167772e-13,6.09392110590618e-13,5.26426855099534e-13,4.51560661911675e-13,3.85035209711022e-13,3.26659888885353e-13,2.75963800596091e-13,2.32312538626243e-13,1.94993825660052e-13,1.6327739327385e-13,1.36454607669149e-13,1.13862821773537e-13,9.48986450258558e-14,7.90234812351253e-14,6.57639070546331e-14,5.47087993909825e-14,4.550458241519e-14,3.78495466833523e-14,3.14878780626991e-14,2.62038038531064e-14,2.18160995545785e-14,1.81730862890955e-14,1.51481728546346e-14,1.26359474138532e-14,1.05487939564499e-14,8.81399198329408e-15,7.37124999882222e-15],[9.085975378499e-24,5.57962259579032e-21,5.43341042814069e-19,1.57259148402345e-17,1.97223283934066e-16,1.36116752180562e-15,6.05688574348602e-15,1.93725973295201e-14,4.80970280569167e-14,9.80059400646575e-14,1.70814673789743e-13,2.62705499834278e-13,3.65141263285789e-13,4.67272639978927e-13,5.58666542513781e-13,6.31348009806685e-13,6.80753106598533e-13,7.05698340179524e-13,7.07718750107386e-13,6.90149160891946e-13,6.57226754717072e-13,6.13368733171438e-13,5.62676354257119e-13,5.08651718085954e-13,4.54082727828286e-13,4.01044143294214e-13,3.50968096253058e-13,3.04748133922784e-13,2.62852149160695e-13,2.25429178454181e-13,1.92402264276512e-13,1.63544470337238e-13,1.3853813898973e-13,1.17019099501587e-13,9.86082308463775e-14,8.29329101662339e-14,6.96406926313902e-14,5.84072382770613e-14,4.89401295536097e-14,4.09798673316015e-14,3.42990208213013e-14,2.87002480347707e-14,2.40136975707528e-14,2.00941440772569e-14,1.68180911995617e-14,1.40809893834754e-14,1.17946544796853e-14,9.88493063724844e-15,8.28961256072118e-15,6.95662396371784e-15,5.84243801573847e-15],[1.01566947617687e-24,8.43807699820905e-22,1.03311557720449e-19,3.57791487847236e-18,5.18444896516177e-17,4.02934329059561e-16,1.98029278116038e-15,6.89145447746466e-15,1.8396763259322e-14,3.99249653987021e-14,7.35390150277749e-14,1.18762577952845e-13,1.72410591948724e-13,2.29405113736874e-13,2.84081562101213e-13,3.31421614852391e-13,3.6785857195825e-13,3.91568272613185e-13,4.02344466767611e-13,4.01230250142759e-13,3.90067031601601e-13,3.71073858175247e-13,3.46516128582782e-13,3.18480678294115e-13,2.88748312555803e-13,2.58742844030361e-13,2.29533100520808e-13,2.0186697447633e-13,1.76221300452254e-13,1.52856294671403e-13,1.31867541875252e-13,1.13231750468774e-13,9.68447368544077e-14,8.25515133445562e-14,7.016915030601e-14,5.95034552210726e-14,5.03606141315586e-14,4.25548880830253e-14,3.59133261428836e-14,3.02782965567613e-14,2.55084775415413e-14,2.14788042716023e-14,1.80797452541962e-14,1.52161807928567e-14,1.28060770885272e-14,1.07790889211098e-14,9.07517859442455e-15,7.64330582792296e-15,6.44021980087044e-15,5.42936829845411e-15,4.57992801335741e-15]],"type":"surface","frame":null}],"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script> --- class: clear Another example .pull-left[ <img src="gibbs_files/figure-html/mnorm_persp-1.png" width="95%" style="display: block; margin: auto;" /> ] .pull-right[ <img src="gibbs_files/figure-html/condprob-1-1.png" width="95%" style="display: block; margin: auto;" /> ] --- class: clear .font70[ ### 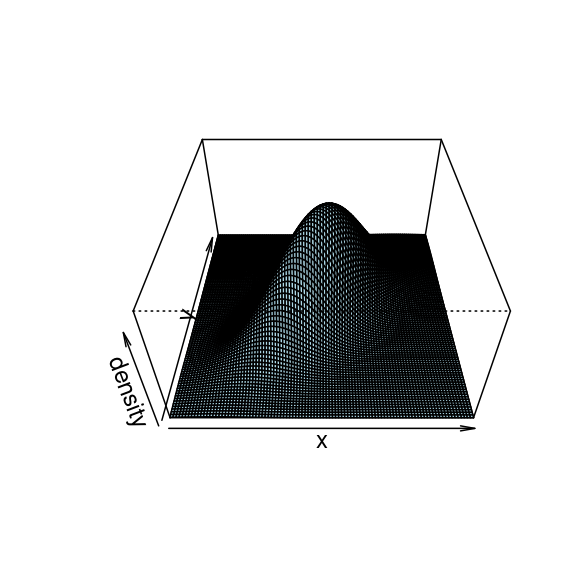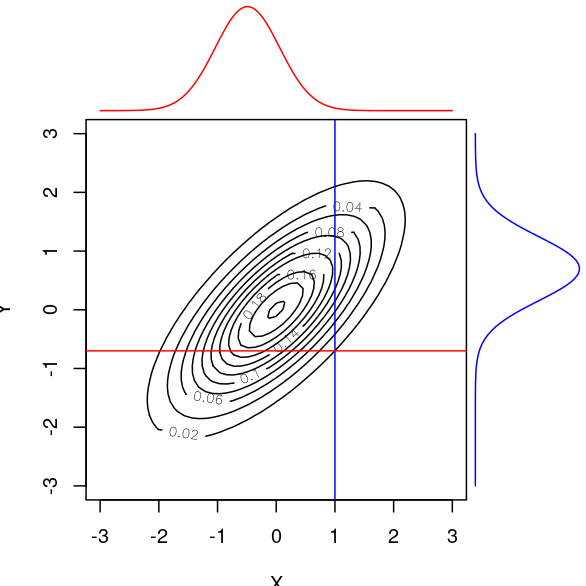Conjugate priors for conditional distributions `\begin{align} \mu & \sim N(\mu_0, \tau_0^2) \\ \sigma^2 & \sim \text{Inv-Gamma}(\nu_0 / 2, \nu_0 \sigma^2_0 / 2) \end{align}` - `\(\mu_0\)`: Prior mean, `\(\tau_0^2\)`; Prior variance (i.e., uncertainty) of the mean - `\(\nu_0\)`: Prior sample size for the variance; `\(\sigma^2_0\)`: Prior expectation of the variance ### Posterior `\begin{align} \mu \mid \sigma^2, y & \sim N(\mu_n, \tau_n^2) \\ \sigma^2 \mid \mu & \sim \text{Inv-Gamma}(\nu_n / 2, \nu_n \sigma^2_n [\mu] / 2) \end{align}` - `\(\tau_n^2 = \left(\frac{1}{\tau_0^2} + \frac{n}{\sigma^2}\right)^{-1}\)`; `\(\mu_n = \tau_n^2 \left(\frac{\mu_0}{\tau_0^2} + \frac{n \bar y}{\sigma^2}\right)\)` - `\(\nu_n = \nu_0 + n\)`; `\(\sigma^2_n (\mu) = \frac{1}{\nu_n} \left[\nu_0 \sigma^2_0 + (n - 1) s^2_y + \sum (\bar y - \mu)^2\right]\)` ] --- class: clear No need for a separate proposal distribution; directly sample the conditional posterior - Thus, all draws are accepted -- ### Posterior Summary 2 chains, 10,000 draws each, half warm-ups `\(\mu_0\)` = 5, `\(\sigma^2_0\)` = 1, `\(\tau^2_0\)` = 100, `\(\nu_0\)` = 1 .font70[ |variable | mean| median| sd| mad| q5| q95| rhat| ess_bulk| ess_tail| |:--------|----:|------:|-----:|-----:|-----:|----:|----:|--------:|--------:| |mu | 3.1| 3.10| 0.213| 0.211| 2.753| 3.45| 1| 9928| 9936| |sigma2 | 1.4| 1.33| 0.378| 0.337| 0.904| 2.11| 1| 10189| 10136| ] The ESS is almost as large as # of draws