Markov Chain Monte Carlo

class: center, middle, inverse, title-slide

# Markov Chain Monte Carlo
## PSYC 573
### University of Southern California
### February 10, 2022

---

class: inverse, center, middle

# Monte Carlo

---

# Monte Carlo (MC) Methods

.pull-left[

![](https://upload.wikimedia.org/wikipedia/commons/3/36/Real_Monte_Carlo_Casino.jpg)

]

???

Image credit: [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:Real_Monte_Carlo_Casino.jpg)

.pull-right[
.font70[

- 1930s and 40s: answer questions in nuclear physics not solvable with conventional mathematical methods
    * Key figures: Stanislaw Ulam, John von Neumann, Nicholas Metropolis

- Central element of the Manhattan Project in the development of the hydrogen bomb

]
]

---

# MC With One Unknown

`rbeta()`, `rnorm()`, `rbinom()`: generate values that imitate *independent samples* from known distributions

- use *pseudorandom* numbers

.font70[
E.g., `rbeta(n, shape1 = 15, shape2 = 10)`
]

---
class: clear

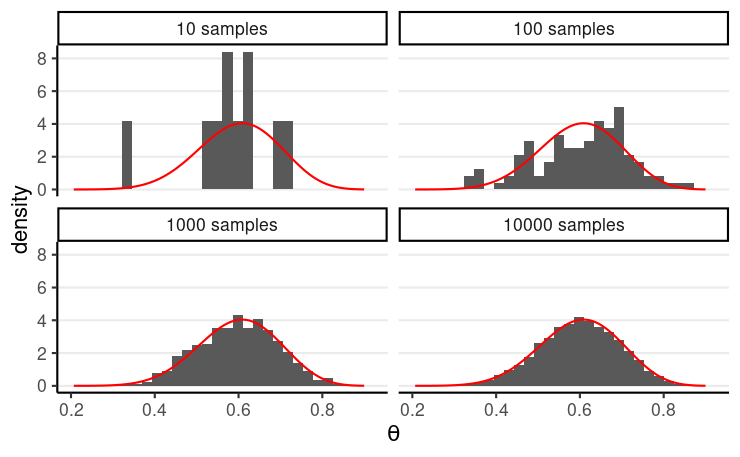
With a large number of draws (`$S$`),

- sample density `$\to$` target distribution
- most sample statistics (e.g., mean, quantiles) `$\to$` corresponding characteristics of the target density

---
class: inverse, middle, center

# Markov Chain Monte Carlo

---

# MCMC

Main problem in Bayesian: no way to draw independent samples from posterior
`$$P(\theta \mid y) = \frac{\mathrm{e}^{-(\theta - 1 / 2)^2} 
                                     \theta^y (1 - \theta)^{n - y}}
                       {\int_0^1 \mathrm{e}^{-(\theta^* - 1 / 2)^2} 
                        {\theta^*}^y (1 - {\theta^*})^{n - y} d\theta^*}$$`

MCMC: draw *dependent (correlated)* samples without evaluating the integral in the denominator

---
class: clear

- Some commonly used algorithms:
    * The Metropolis algorithm (also called *random-walk* Metropolis)
    * Gibbs sampling (in BUGS, JAGS)
    * Hamiltonian Monte Carlo (and No-U-Turn sampler; in STAN)

---
class: inverse, middle, center

# The Metropolis Algorithm

---
exclude: TRUE
class: clear

![](images/Metropolis_algorithm.png)

---

# An Analogy

.pull-left[

![](https://upload.wikimedia.org/wikipedia/commons/2/29/LA_districts_map.png)

]

.pull-right[

.font70[

You have a task: tour all regions in LA county, and the time your spend on each region should be proportional to its popularity

However, you don't know which region is the most popular

Each day, you will decide whether to stay in the current region or move to a neighboring region

You have a tour guide that tells you whether region A is more or less popular than region B and by how much

> How would you proceed?

]
]

???

Image credit: [Wikimedia Commons](https://commons.wikimedia.org/wiki/File:LA_districts_map.png)

---
class: clear

### Using the Metropolis Algorithm

1. On each day, randomly select a new region
2. If the *proposed* region is *more popular* than the current one, definitely go to the new region
3. If the *proposed* region is *less popular* than the current one, go to the new region with  
    `$P(\text{accept the new region}) = \frac{\text{proposed region popularity}}{\text{current region popularity}}$`
    - E.g., by spinning a wheel

In the long run, distribution of time spent in each region = distribution of popularity of each region

---

# Demonstration

```r
shiny::runGitHub("metropolis_demo", "marklhc")
```

---
class: inverse, middle, center

# Example 1: Estimating the Number of People Taking the Metro

---
class: clear

Data from LA Barometer (by the USC Dornsife Center for Economic and Social Research)

338 first-gen immigrants, 86 used the metro in the previous year

Question:

> What proportion of first-gen immigrants uses the metro in a year?

.footnote[

Press release: https://dornsife.usc.edu/news/stories/3164/labarometer-mobility-in-los-angeles-survey/

]

---

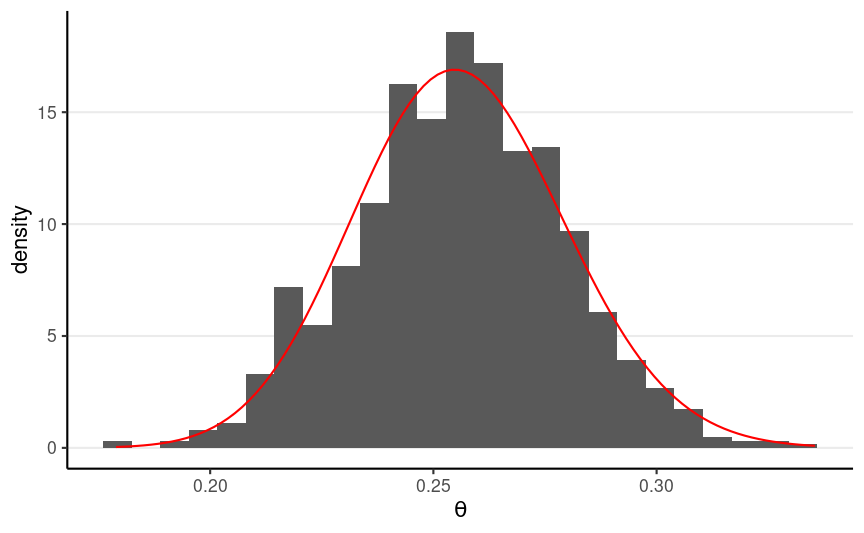
# Analytic Method

Beta(1.5, 2) prior `$\to$` Beta(87.5, 254) posterior

1,000 independent draws from the posterior:

---

# With the Metropolis Algorithm

Proposal density: `$N(0, 0.1)$`; Starting value: `$\theta^{(1)} = 0.1$`

.footnote[

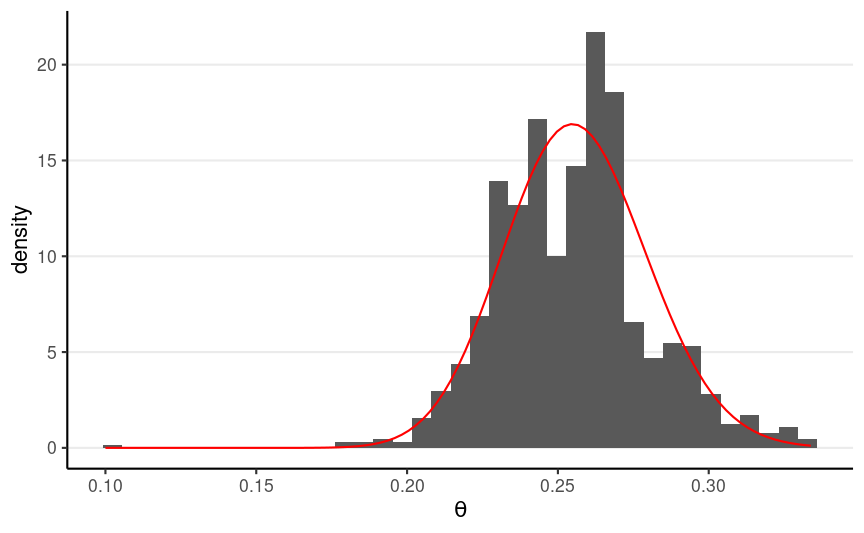
R code for running the algorithm can be found in the note

]

---
class: clear

With enough *iterations*, the Metropolis will simulate samples from the target distribution

It is *less efficient* than `rbeta` because the draws are *dependent*

> Pros: 
> - does not require solving the integral
> - can use non-conjugate priors
> - easy to implement

> Cons:
> - not efficient; not scalable in complex models
> - require tuning the proposal SD;

---
class: inverse, center, middle

# MCMC Diagnostics

---

# Markov Chain

Markov chain: a sequence of iterations, `$\{\theta^{(1)}, \theta^{(2)}, \ldots, \theta^{(S)}\}$`

- the "state" `$\theta^{(s)}$` depends on `$\theta^{(s - 1)}$`
    * where to travel next depends on where the current region is

Based on *ergodic* theorems, a well-behaved chain will reach a *stationary distribution*

- after which, every draw is a sample from the stationary distribution

---
exclude: TRUE
class: clear

Exercise:

1. Try using different proposal SD: 0.02, 0.1, 0.3, 1
2. For each, draw 1,000 samples
3. Does the sample distribution look like the target posterior?
4. What is the relationship between proposal SD, acceptance rate, and autocorrelation?
5. Which proposal SD seems to give the best effective sample size?

---

# Warm-up

It takes a few to a few hundred thousand iterations for the chain to get to the stationary distribution

Therefore, a common practice is to discard the first `$S_\text{warm-up}$` (e.g., first half of the) iterations
- Also called *burn-in*

---
class: clear

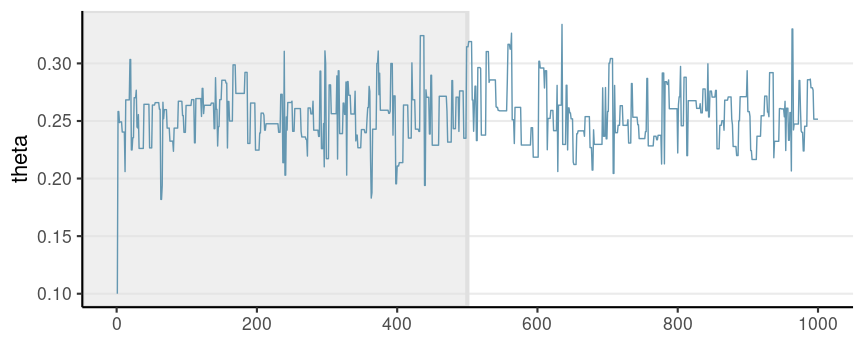
## When Can We Use MCMC Draws to Approximate the Posterior?

1. The draws need to be *representative* of the posterior
2. The draws contain sufficient information to *accurately* describe the posterior

### Tools

- Trace plots/Rank histograms
- `$\hat R$`
- Effective sample size (ESS)

---

# Representativeness

The chain does not get stuck

*Mixing*: multiple chains cross each other

---

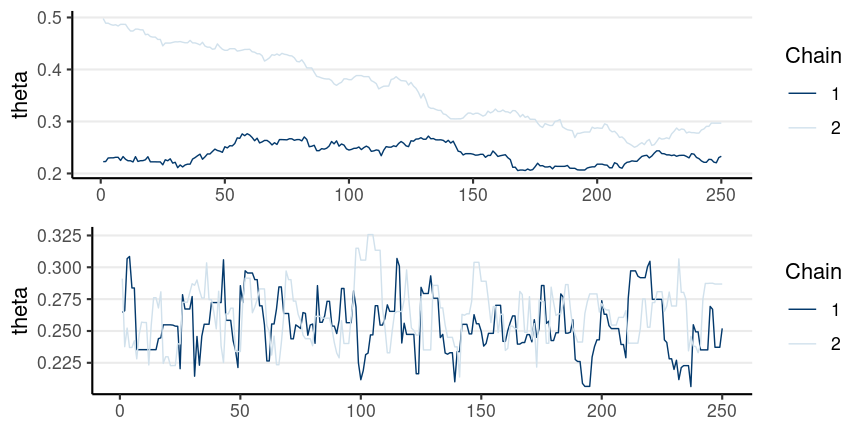
# Representativeness

For more robust diagnostics (Vehtari et al., 2021, doi: [10.1214/20-BA1221](https://doi.org/10.1214/20-BA1221))

- The rank histograms should look like uniform distributions

---

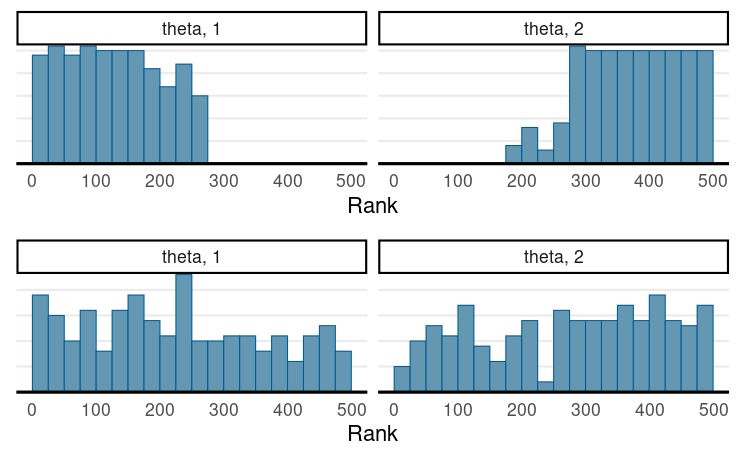
# Representativeness

`$$\hat{R} = \frac{\text{Between-chain variance} + \text{within-chain variance}}
                 {\text{within-chain variance}}$$`
- aka: *Gelman-Rubin statistic*, the *potential scale reduction factor*

When the chains converge, each should be exploring the same stationary distribution

- No between-chain differences `$\Rightarrow$` `$\hat{R} \to 1$`
- Vehtari et al. (2021) recommended `$\hat{R} < 1.01$` for convergence

---
class: clear

In the previous examples,

- `$\hat R$` = 2.044 for the poor mixing graph
- `$\hat R$` = 1.033 for the good mixing graph

---

# Effective Sample Size (ESS)

MCMC draws are dependent, so they contain less information for the target posterior distribution

> What is the equivalent number of draws if the draws were independent?

- E.g., ESS = 98.289 for the good mixing example
    * Need ~5087.022 draws to get equal amount of information as 1,000 independent samples

---
class: clear

### Heuristics for ESS

- ESS (bulk and tail) > 400 to interpret `$\hat R$` (Vehtari et al., 2021)
- ESS > 1000 for stable summary of the posterior
    * Kruschke (2015) recommended 10,000

---

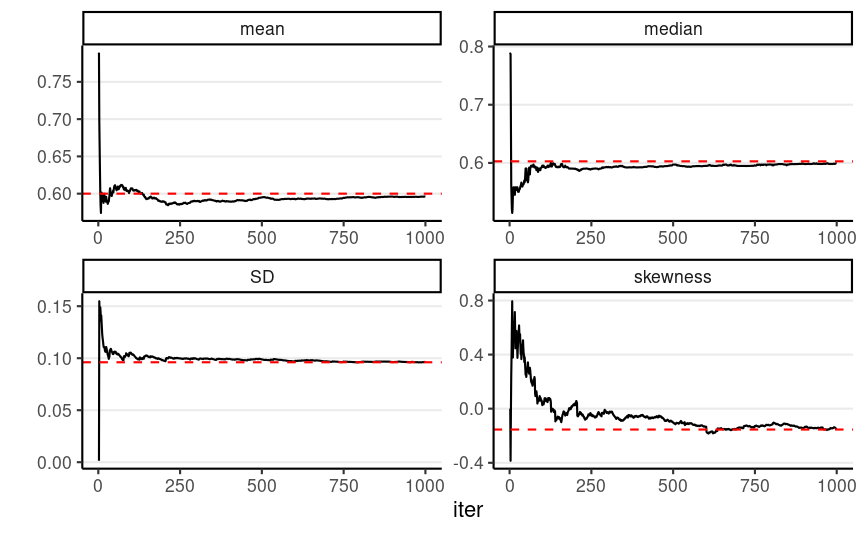
# Sample Convergence Paragraph

.font70[

> We used Markov Chain Monte Carlo (MCMC), specifically a Metropolis algorithm implemented in R, to approximate the posterior distribution of the model parameters. We used two chains, each with 10,000 draws. The first 5,000 draws in each chain were discarded as warm-ups. Trace plots of the posterior samples (Figure X) showed good mixing, and `$\hat R$` statistics (Vehtari et al., 2021) were < 1.01 for all model parameters, indicating good convergence for the MCMC chains. The effective sample sizes > 2376.931 for all model parameters, so the MCMC draws are sufficient for summarizing the posterior distributions.

]

---

# Sample Results

> The model estimated that 25.569% (posterior SD = 2.328%, 90% CI [21.813%, 29.467%]) of first-generation immigrants took the metro in the year 2019.

---

# Things to Remember
    
- MCMC draws dependent/correlated samples to approximate a posterior distribution
    * ESS < `$S$`
- It needs warm-up iterations to reach a stationary distribution
- Check for representativenes
    * Trace/Rank plot and `$\hat{R}$`
- Need large ESS to describe the posterior accurately