Introduction
PSYC 573
University of Southern California
January 11, 2022
History of Bayesian Statistics
- Video intro: https://www.youtube.com/watch?v=BcvLAw-JRss
- A nice popular science book by Sharon Bertsch McGrayne: The theory that would not die
Historical Figures
Thomas Bayes (1701--1762)

- English Presbyterian minister
- "An Essay towards solving a Problem in the Doctrine of Chances", edited by Richard Price after Bayes's death
Pierre-Simon Laplace (1749--1827)

- French Mathematician
- Formalize Bayesian interpretation of probability, and most of the machinery for Bayesian statistics
Image credit: Wikimedia Commons, Wikimedia Commons
In the 20th Century
Bayesian---way to do statistics until early 1920s
Ronald Fisher and Frequentist scholars took over
- "The theory of inverse probability is founded upon an error, and must be wholly rejected" (Fisher, 1925, p. 10)1
[1]: Aldrich, J. (2008). R. A. Fisher on Bayes and Bayes' theorem. Bayesian Analysis, 3(1), 161--170.
Resurrection

Alan Turing's algorithms in code breaking in World War II
Markov Chain Monte Carlo (MCMC) algorithm
- Bring Bayesian back to the main stream of statistics
Image credit: Wikimedia Commons
Why Should You Learn About the Bayesian Way?
- Gigerenzer (2004): It is one tool of your statistical toolbox
Why Should You Learn About the Bayesian Way?
Gigerenzer (2004): It is one tool of your statistical toolbox
Increasingly used as alternative to frequentist statistics
Why Should You Learn About the Bayesian Way?
Gigerenzer (2004): It is one tool of your statistical toolbox
Increasingly used as alternative to frequentist statistics
Computationally more stable for complex models
Why Should You Learn About the Bayesian Way?
Gigerenzer (2004): It is one tool of your statistical toolbox
Increasingly used as alternative to frequentist statistics
Computationally more stable for complex models
A coherent way of incorporating prior information
- Common sense knowledge, previous literature, sequential experiments, etc
Bayesian Idea 1
Reallocation of credibility across possibilities
Hypothetical example: How effective is a vaccine?
Bayesian Idea 1
Reallocation of credibility across possibilities
Hypothetical example: How effective is a vaccine?
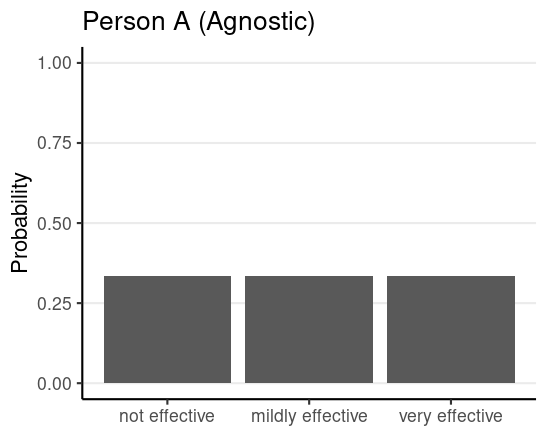
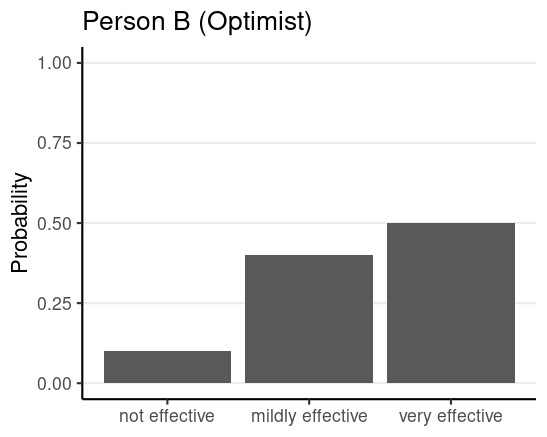
Prior (before collecting data)
Updating Beliefs
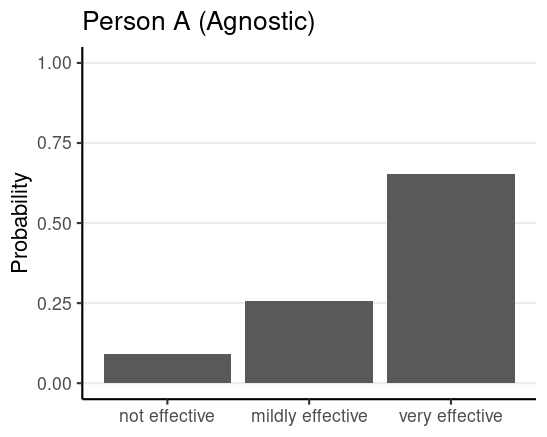
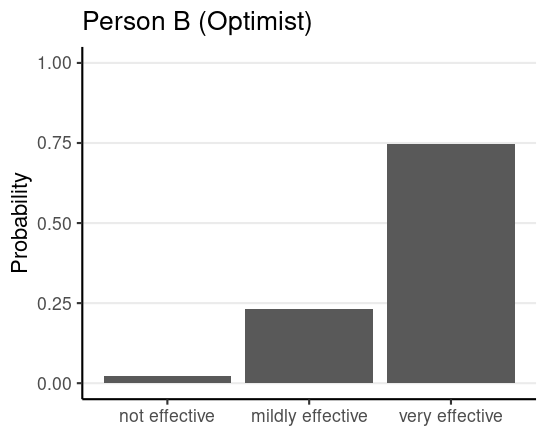
After seeing results of a trial
- 4/5 with the vaccince improved
- 2/5 without the vaccine improved
Updating Beliefs
After seeing results of a trial
- 4/5 with the vaccince improved
- 2/5 without the vaccine improved
Possibilities = Parameter Values
- Parameter: Effectiveness of the vaccine
- Possibilities: Not effective, mildly effective, very effective
Here the parameter is a discrete variable
Possibilities = Parameter Values
- Parameter: Effectiveness of the vaccine
- Possibilities: Not effective, mildly effective, very effective
Here the parameter is a discrete variable
- Parameter: Risk reduction by taking the vaccine
- Possibilities: (−∞,∞) (Any real number)
Here the parameter is a continuous variable
Using Bayesian analysis, one obtains updated/posterior probability for every possibility of a parameter, given the prior belief and the data
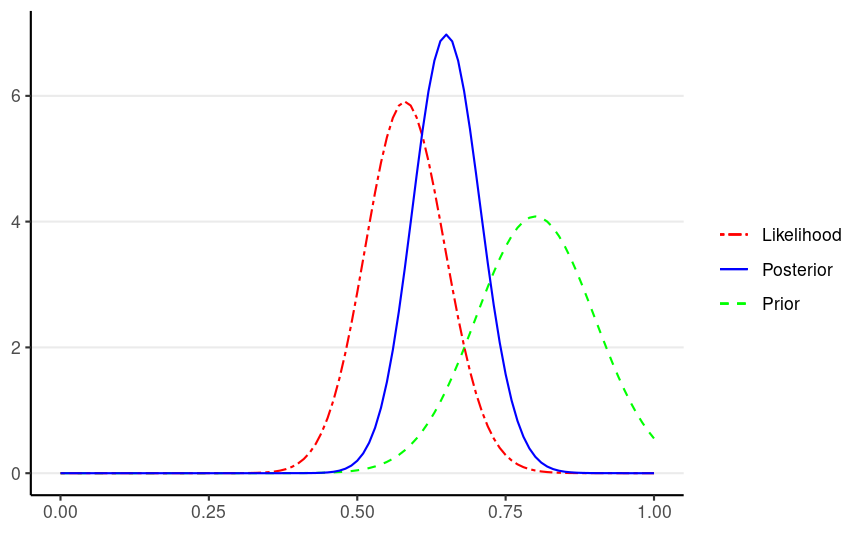
Steps of Bayesian Data Analysis
"Turning the Bayesian crank"
- Identify data
- Define a mathematical model with parameters
- Specify priors on parameters
- Obtain and interpret posterior distributions of the parameters
- Posterior predictive check
Example
Frank et al. (2019, Cognition and Emotion)
- Response time for 2 (Dutch--native vs. English--foreign) × 2 (lie vs. truth) experimental conditions
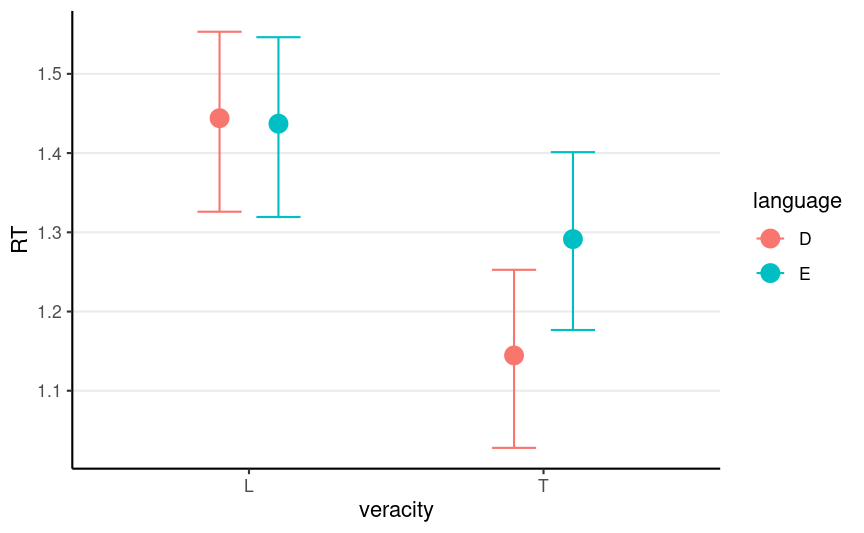
Posterior of Mean RTs by Conditions
L = Lie, T = Truth; D = Dutch, E = English
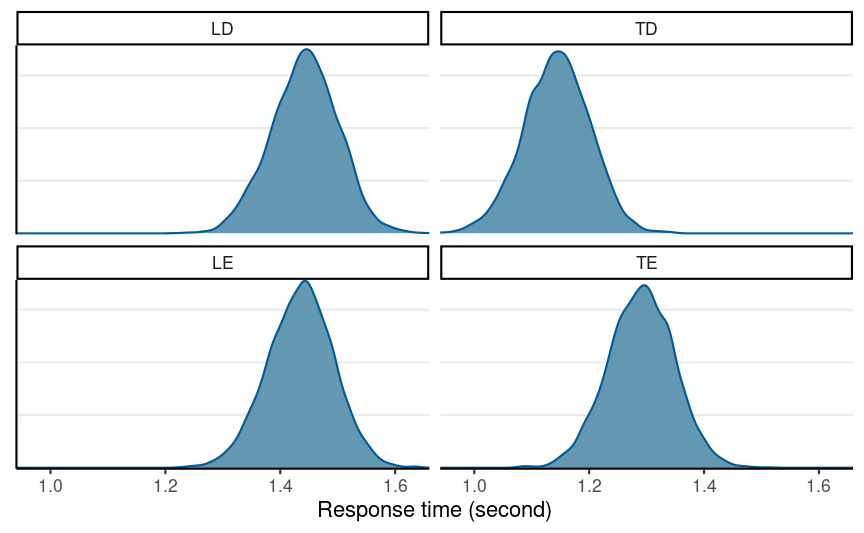
From Priors to Posteriors
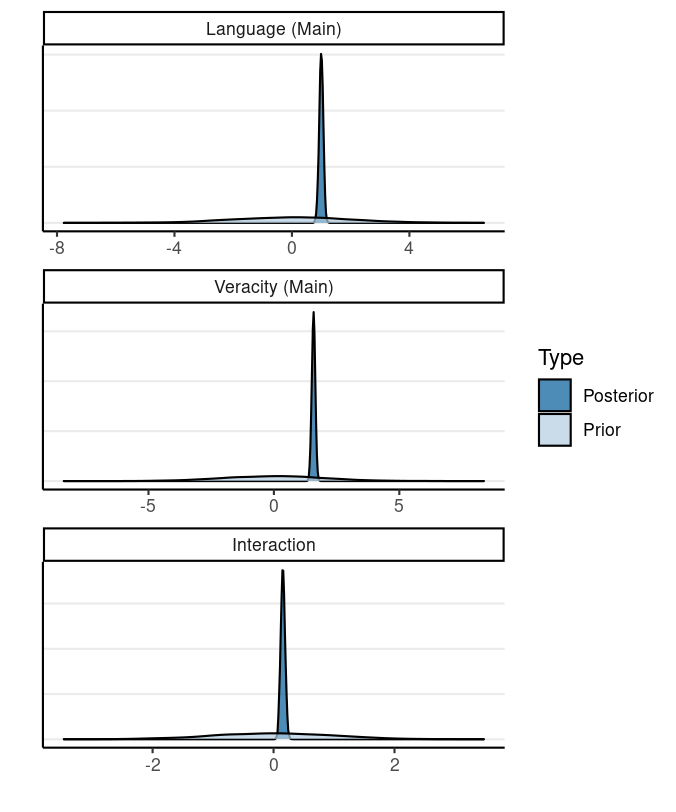
Accepting the Null
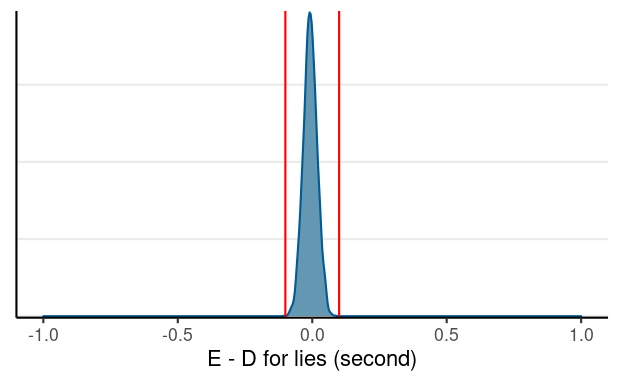
Accepting the Null

Posterior Predictive Check
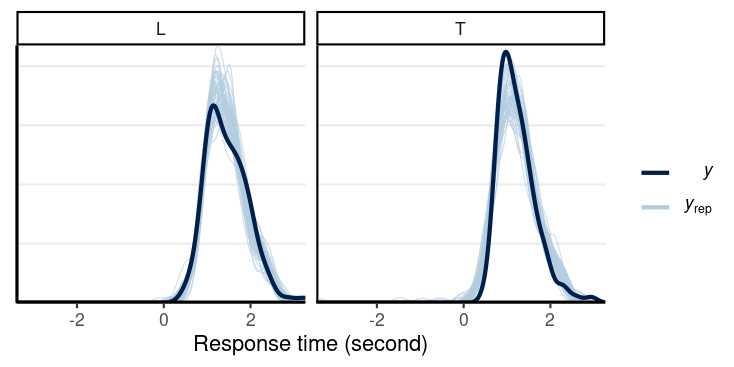
Multiple Experiments
Kay, Nelson, & Hekler (2016, p. 4525, https://dl.acm.org/doi/abs/10.1145/2858036.2858465)