Causal Inference
PSYC 573
University of Southern California
March 29, 2022
Causation
Data are profoundly dumb about causal relationships
--- Pearl & Mackenzie (2018)
Outline:
- DAG
- confounding
- d-separation
- mediation
Materials based on chapters 5 and 6 of McElreath (2020)
Causal Inference
Obtaining an estimate of the causal effect of one variable on another
Causal Inference
Obtaining an estimate of the causal effect of one variable on another
an hour more exercise per day causes an increase in happiness by 0.1 to 0.2 points
Causal Inference
Obtaining an estimate of the causal effect of one variable on another
an hour more exercise per day causes an increase in happiness by 0.1 to 0.2 points
- Intervention: if I exercise one hour more, my happiness will increase by 0.1 to 0.2 points
- Counterfactual: had I exercised one less hour, my happiness would have been 0.1 to 0.2 points less
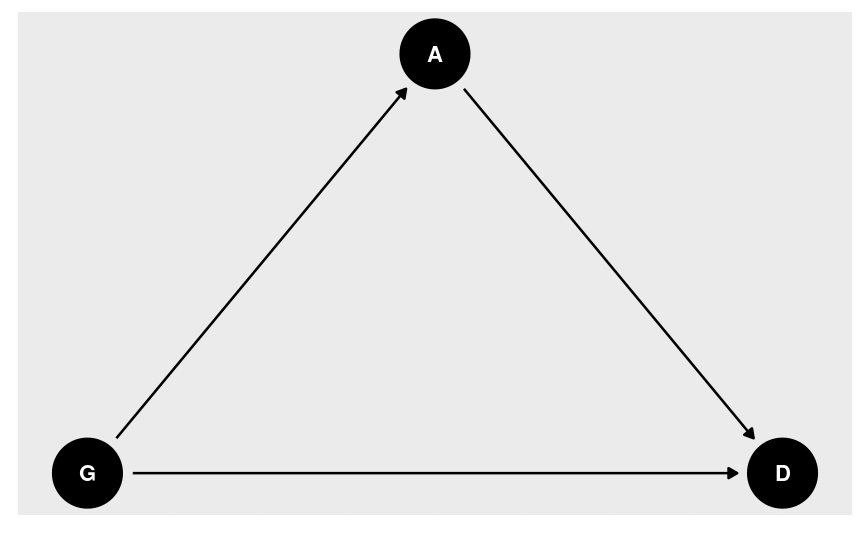
Directed Acyclic Graph
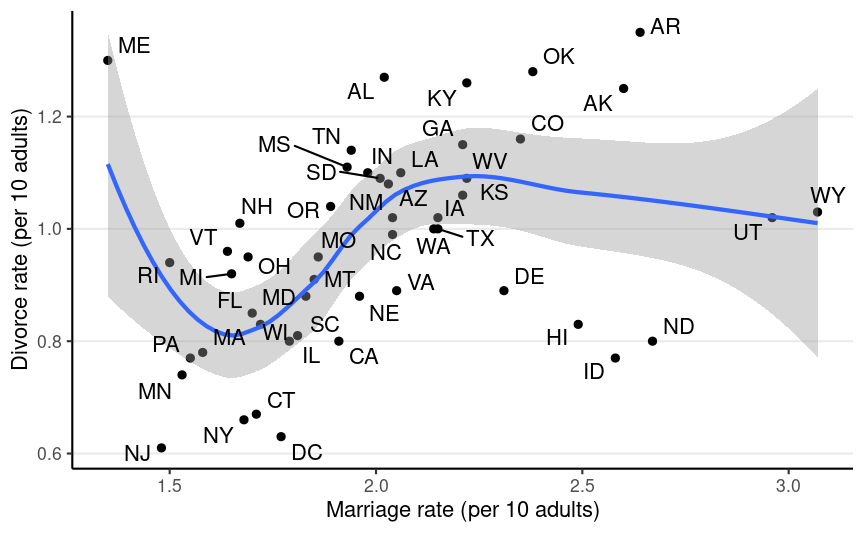
Data from the 2009 American Community Survey (ACS)
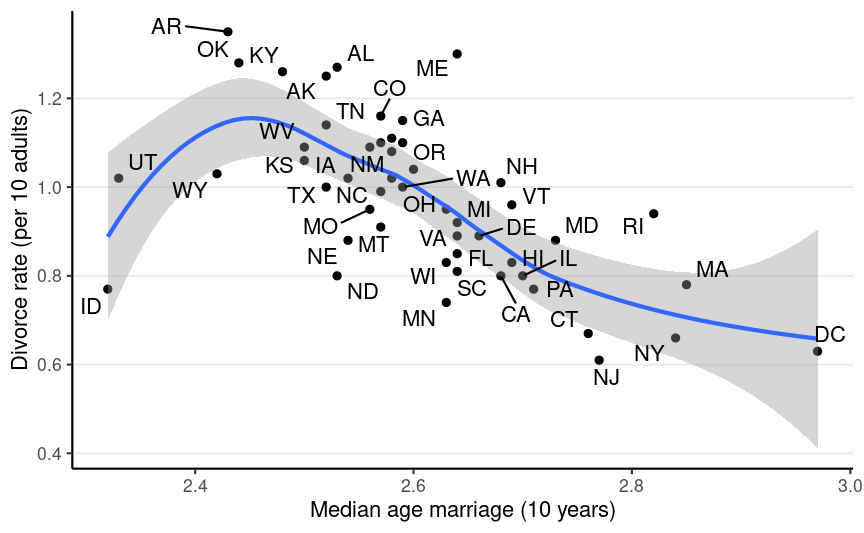
Data from the 2009 American Community Survey (ACS)

Does marriage cause divorce? (pay attention to the unit of analysis)
Age at marriage?
Directed Acyclic Graph (DAG)
Allows researchers to encode causal assumptions of the data
- Based on knowledge of the data and the variables
Directed Acyclic Graph (DAG)
Allows researchers to encode causal assumptions of the data
- Based on knowledge of the data and the variables
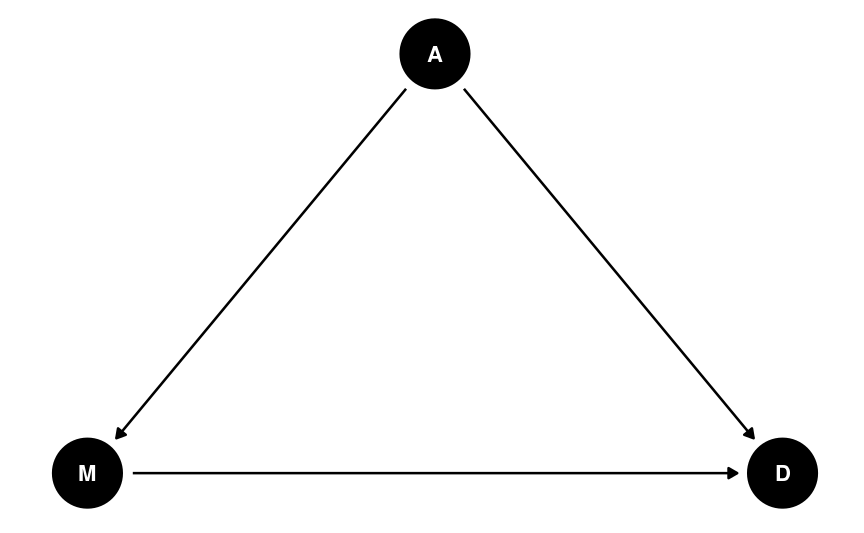
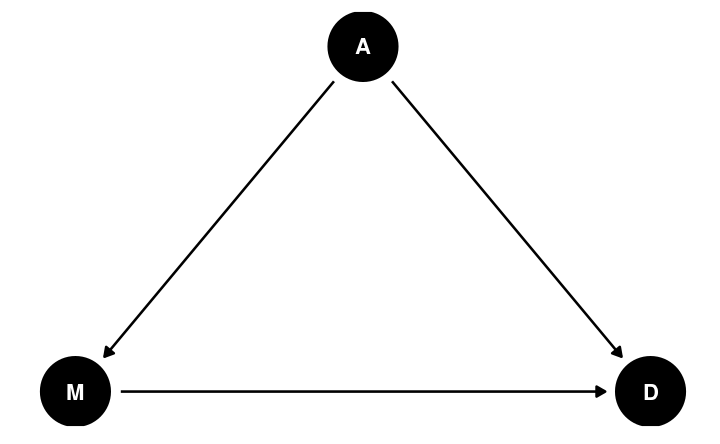

"Weak" assumptions
- A may directly influence M
- A may directly influence D
- M may directly influence D

"Weak" assumptions
- A may directly influence M
- A may directly influence D
- M may directly influence D
"Strong" assumptions: things not shown in the graph
- E.g., M does not directly influence A
- E.g., A is the only relevant variable in the causal pathway M → D
Basic Types of Junctions
Fork: A ← B → C
Chain/Pipe: A → B → C
Collider: A → B ← C
Fork
aka Classic confounding
- Confound: something that misleads us about a causal influence
M ← A → D
Fork
aka Classic confounding
- Confound: something that misleads us about a causal influence
M ← A → D
Assuming the DAG is correct,
- the causal effect of M → D can be obtained by holding constant A
- stratifying by A; "controlling" for A
Di∼N(μi,σ)μi=β0+β1Ai+β2Miβ0∼N(0,5)β1∼N(0,1)β2∼N(0,1)σ∼t+4(0,3)
library(brms)m1 <- brm(Divorce ~ MedianAgeMarriage + Marriage, data = waffle_divorce, prior = prior(std_normal(), class = "b") + prior(normal(0, 5), class = "Intercept") + prior(student_t(4, 0, 3), class = "sigma"), seed = 941, iter = 4000)># Family: gaussian ># Links: mu = identity; sigma = identity ># Formula: Divorce ~ MedianAgeMarriage + Marriage ># Data: waffle_divorce (Number of observations: 50) ># Draws: 4 chains, each with iter = 4000; warmup = 2000; thin = 1;># total post-warmup draws = 8000># ># Population-Level Effects: ># Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS># Intercept 3.49 0.77 1.96 4.99 1.00 5179 5008># MedianAgeMarriage -0.94 0.25 -1.42 -0.44 1.00 5605 5608># Marriage -0.04 0.08 -0.20 0.12 1.00 5198 4900># ># Family Specific Parameters: ># Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS># sigma 0.15 0.02 0.12 0.19 1.00 6071 5326># ># Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS># and Tail_ESS are effective sample size measures, and Rhat is the potential># scale reduction factor on split chains (at convergence, Rhat = 1).Posterior predictive checks
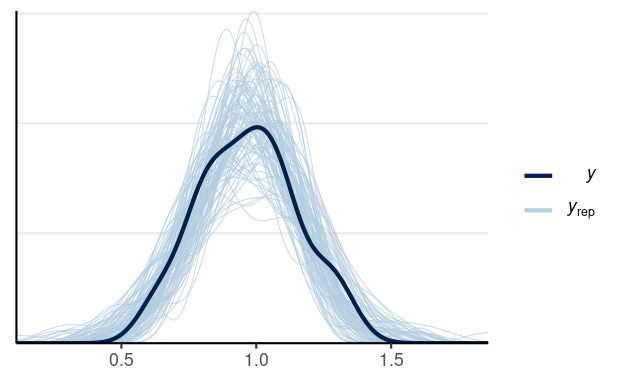
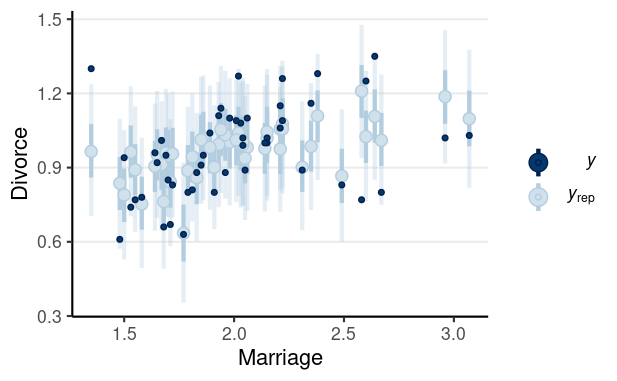
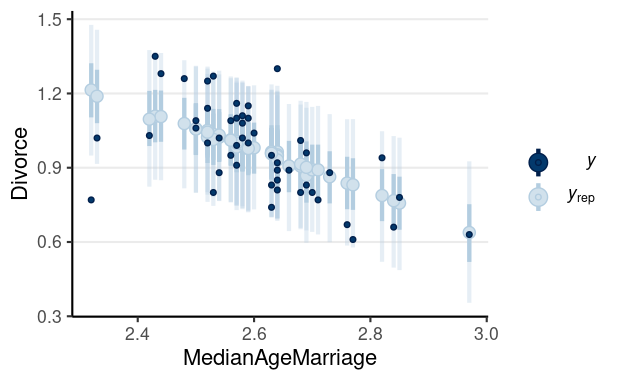
Pedicting an Intervention
What would happen to the divorce rate if we encourage more people to get married, so that marriage rate increases by 1 per 10 adults?
Pedicting an Intervention
What would happen to the divorce rate if we encourage more people to get married, so that marriage rate increases by 1 per 10 adults?
Based on our DAG, this should not change the median marriage age
Pedicting an Intervention
What would happen to the divorce rate if we encourage more people to get married, so that marriage rate increases by 1 per 10 adults?
Based on our DAG, this should not change the median marriage age
| Marriage | MedianAgeMarriage | Estimate | Est.Error | Q2.5 | Q97.5 |
|---|---|---|---|---|---|
| 2 | 2.5 | 1.07 | 0.034 | 0.999 | 1.14 |
| 3 | 2.5 | 1.03 | 0.068 | 0.894 | 1.16 |
Randomization
Framing Experiment
- X: exposure to a negatively framed news story about immigrants
- Y: anti-immigration political action
Framing Experiment
- X: exposure to a negatively framed news story about immigrants
- Y: anti-immigration political action
No Randomization
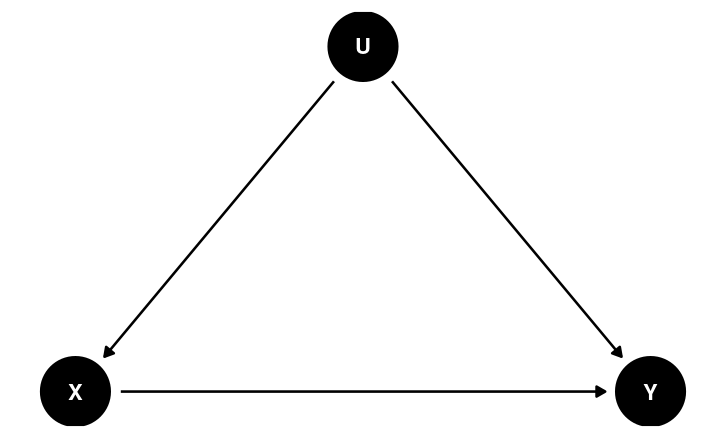
Potential confound:
- Location
- Usual outlet/source to acquire information
Framing Experiment
- X: exposure to a negatively framed news story about immigrants
- Y: anti-immigration political action
No Randomization

Randomization
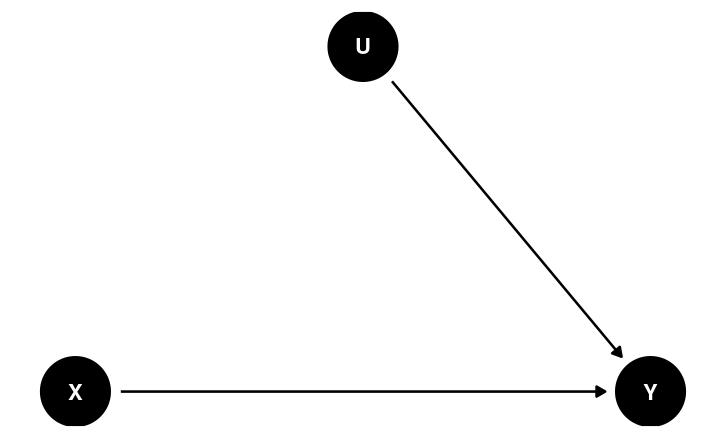
Potential confound:
- Location
- Usual outlet/source to acquire information
Back-Door Criterion
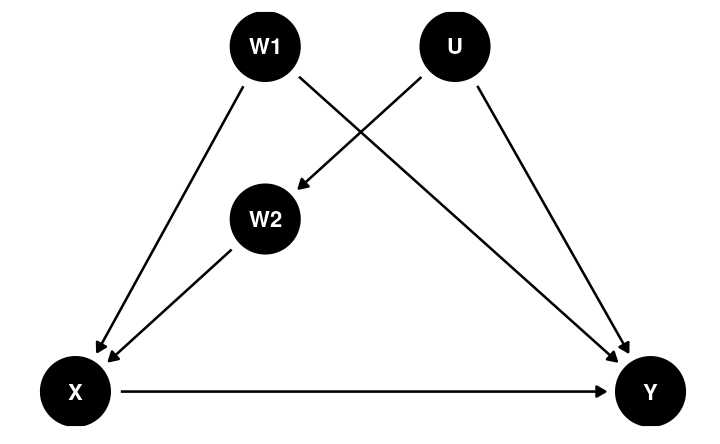
The causal effect of X → Y can be obtained by blocking all the backdoor paths that do not involve descendants of X
Back-Door Criterion

The causal effect of X → Y can be obtained by blocking all the backdoor paths that do not involve descendants of X
- Randomization: (when done successfully) eliminates all paths entering X
- Conditioning (holding constant)
Dagitty
library(dagitty)dag4 <- dagitty("dag{ X -> Y; W1 -> X; U -> W2; W2 -> X; W1 -> Y; U -> Y}")latents(dag4) <- "U"adjustmentSets(dag4, exposure = "X", outcome = "Y", effect = "direct")># { W1, W2 }impliedConditionalIndependencies(dag4)># W1 _||_ W2Post-Treatment Bias
Data for Framing Experiment
cong_mesg: binary variable indicating whether or not the participant agreed to send a letter about immigration policy to his or her member of Congressemo: post-test anxiety about increased immigration (0-9)tone: framing of news story (0 = positive, 1 = negative)
Results
| No adjustment | Adjusting for feeling | |
|---|---|---|
| b_Intercept | −0.81 [−1.18, −0.45] | −2.01 [−2.60, −1.40] |
| b_tone | 0.22 [−0.29, 0.74] | −0.14 [−0.71, 0.42] |
| b_emo | 0.32 [0.21, 0.43] |
Negative framing: emphasizing costs Positive framing: emphasizing benefits
Results
| No adjustment | Adjusting for feeling | |
|---|---|---|
| b_Intercept | −0.81 [−1.18, −0.45] | −2.01 [−2.60, −1.40] |
| b_tone | 0.22 [−0.29, 0.74] | −0.14 [−0.71, 0.42] |
| b_emo | 0.32 [0.21, 0.43] |
Which one estimates the causal effect?
Negative framing: emphasizing costs Positive framing: emphasizing benefits
Mediation
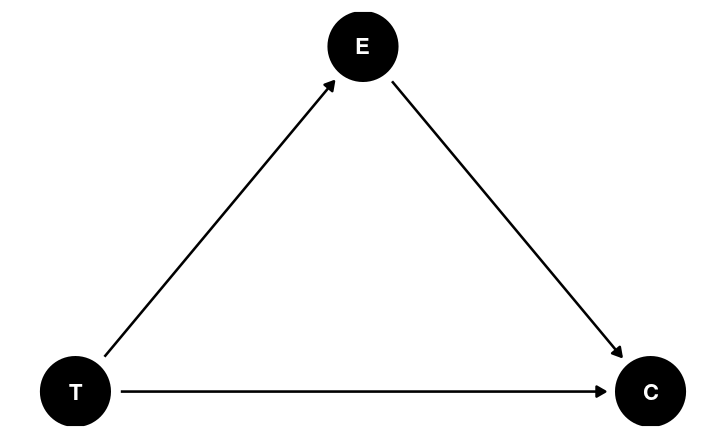
In the DAG, E is a post-treatment variable potentially influenced by T
- E is a potential mediator
Mediation

In the DAG, E is a post-treatment variable potentially influenced by T
- E is a potential mediator
A mediator is very different from a confounder
Mediation Analysis
emoi∼N(μei,σ)μei=βe0+β1toneicong_mesgi∼Bern(μci,σc)logit(μci)=ηiηi=βc0+β2tonei+β3emoiβe0,βc0∼N(0,5)β1,β2,β3∼N(0,1)σ∼t+4(0,3)
m_med <- brm( # Two equations for two outcomes bf(cong_mesg ~ tone + emo) + bf(emo ~ tone) + set_rescor(FALSE), data = framing, seed = 1338, iter = 4000, family = list(bernoulli("logit"), gaussian("identity")))># Family: MV(bernoulli, gaussian) ># Links: mu = logit># mu = identity; sigma = identity ># Formula: cong_mesg ~ tone + emo ># emo ~ tone ># Data: framing (Number of observations: 265) ># Draws: 4 chains, each with iter = 4000; warmup = 2000; thin = 1;># total post-warmup draws = 8000># ># Population-Level Effects: ># Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS># congmesg_Intercept -2.01 0.30 -2.60 -1.42 1.00 9742 6632># emo_Intercept 3.40 0.24 2.93 3.86 1.00 10684 6756># congmesg_tone -0.15 0.29 -0.73 0.41 1.00 9449 6097># congmesg_emo 0.32 0.06 0.21 0.43 1.00 9514 6710># emo_tone 1.14 0.33 0.47 1.79 1.00 10417 5856># ># Family Specific Parameters: ># Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS># sigma_emo 2.73 0.12 2.51 2.98 1.00 10496 6553># ># Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS># and Tail_ESS are effective sample size measures, and Rhat is the potential># scale reduction factor on split chains (at convergence, Rhat = 1).Direct Effect
Causal effect when holding mediator at a specific level
cond_df <- data.frame(tone = c(0, 1, 0, 1), emo = c(0, 0, 9, 9))cond_df %>% bind_cols( fitted(m_med, newdata = cond_df)[ , , "congmesg"] ) %>% knitr::kable()| tone | emo | Estimate | Est.Error | Q2.5 | Q97.5 |
|---|---|---|---|---|---|
| 0 | 0 | 0.122 | 0.032 | 0.069 | 0.195 |
| 1 | 0 | 0.108 | 0.033 | 0.054 | 0.183 |
| 0 | 9 | 0.699 | 0.071 | 0.549 | 0.826 |
| 1 | 9 | 0.669 | 0.063 | 0.539 | 0.786 |
Indirect Effect
Change in Y of the control group if their mediator level changes to what the treatment group would have obtained
Indirect Effect
Change in Y of the control group if their mediator level changes to what the treatment group would have obtained
Quick Demo using posterior means1
- T = 0, E(M) = 3.39
- T = 1, E(M) = 3.39 + 1.14 = 4.53
[1]: Fully Bayesian analyses in the note
Indirect Effect
Change in Y of the control group if their mediator level changes to what the treatment group would have obtained
Quick Demo using posterior means1
- T = 0, E(M) = 3.39
- T = 1, E(M) = 3.39 + 1.14 = 4.53
[1]: Fully Bayesian analyses in the note
| tone | emo | Estimate | Est.Error | Q2.5 | Q97.5 |
|---|---|---|---|---|---|
| 0 | 3.39 | 0.286 | 0.042 | 0.208 | 0.372 |
| 0 | 4.53 | 0.365 | 0.048 | 0.275 | 0.462 |
Potential Confounding
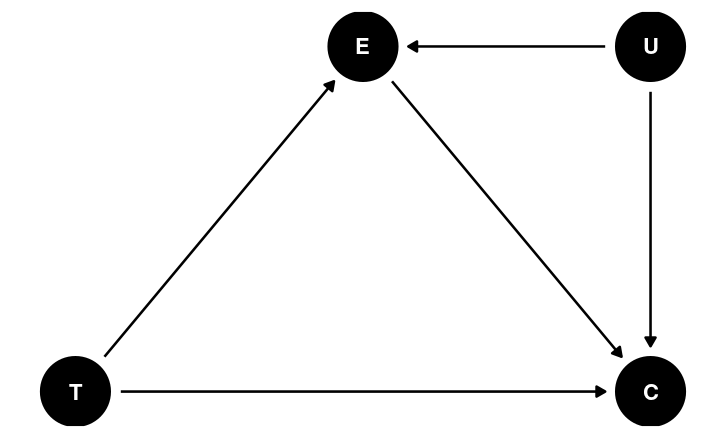
Potential Confounding

Maybe age is related to both emo and cong_mesg?
m_med2 <- brm( # Two equations for two outcomes bf(cong_mesg ~ tone + emo + age) + bf(emo ~ tone + age) + set_rescor(FALSE), data = framing, seed = 1338, iter = 4000, family = list(bernoulli("logit"), gaussian("identity")))Unobserved Confounding
Can be incorporated by assigning priors to the unobserved confounding paths
Collider Bias
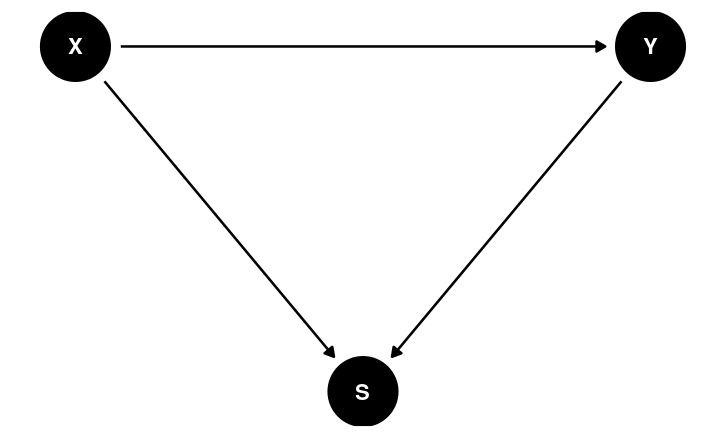
E.g., Is the most newsworthy research the least trustworthy?
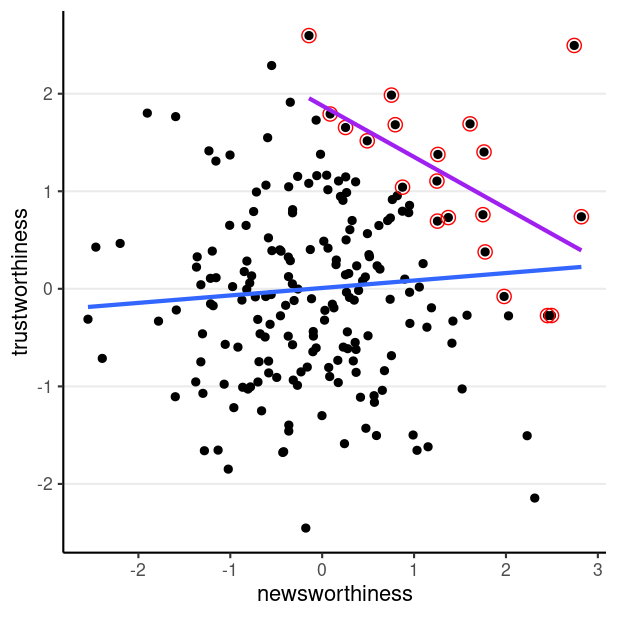
Conditioning on a collider creates spurious associations
- nice person → date ← good-looking person
Conditioning on a collider creates spurious associations
nice person → date ← good-looking person
impulsivity → high-risk youth ← delinquency
Conditioning on a collider creates spurious associations
nice person → date ← good-looking person
impulsivity → high-risk youth ← delinquency
healthcare worker → COVID-19 testing ← COVID-19 severity2
Conditioning on a collider creates spurious associations
nice person → date ← good-looking person
impulsivity → high-risk youth ← delinquency
healthcare worker → COVID-19 testing ← COVID-19 severity2
- standardized test → admission ← research skills
Conditioning on a collider creates spurious associations
nice person → date ← good-looking person
impulsivity → high-risk youth ← delinquency
healthcare worker → COVID-19 testing ← COVID-19 severity2
standardized test → admission ← research skills
maternal smoking → birth weight → birth defect ← mortality
Final Example
Student Admissions at UC Berkeley (1973)
| Dept | App_Male | Admit_Male | Percent_Male | App_Female | Admit_Female | Percent_Female |
|---|---|---|---|---|---|---|
| A | 825 | 512 | 62.1 | 108 | 89 | 82.41 |
| B | 560 | 353 | 63.0 | 25 | 17 | 68.00 |
| C | 325 | 120 | 36.9 | 593 | 202 | 34.06 |
| D | 417 | 138 | 33.1 | 375 | 131 | 34.93 |
| E | 191 | 53 | 27.7 | 393 | 94 | 23.92 |
| F | 373 | 22 | 5.9 | 341 | 24 | 7.04 |
| Total | 2691 | 1198 | 44.5 | 1835 | 557 | 30.35 |
Causal Thinking
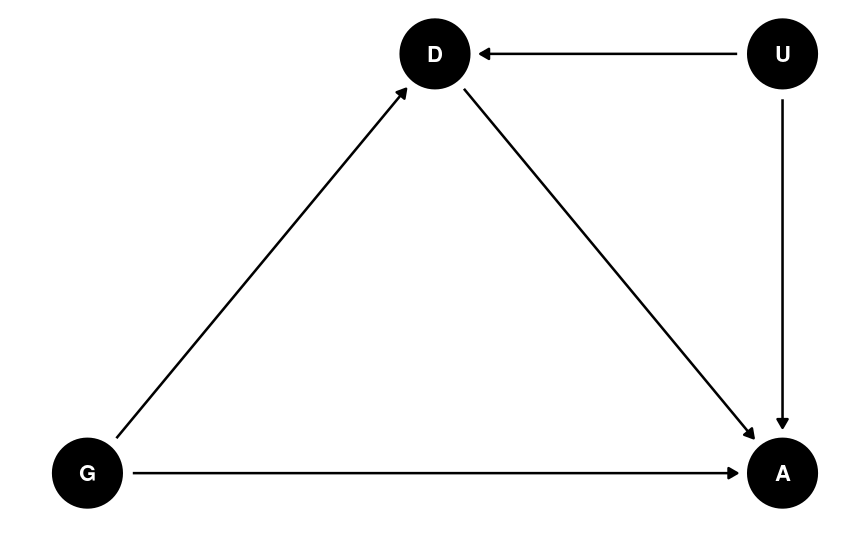
What do we mean by the causal effect of gender?
What do we mean by gender bias?
Instrumental Variables
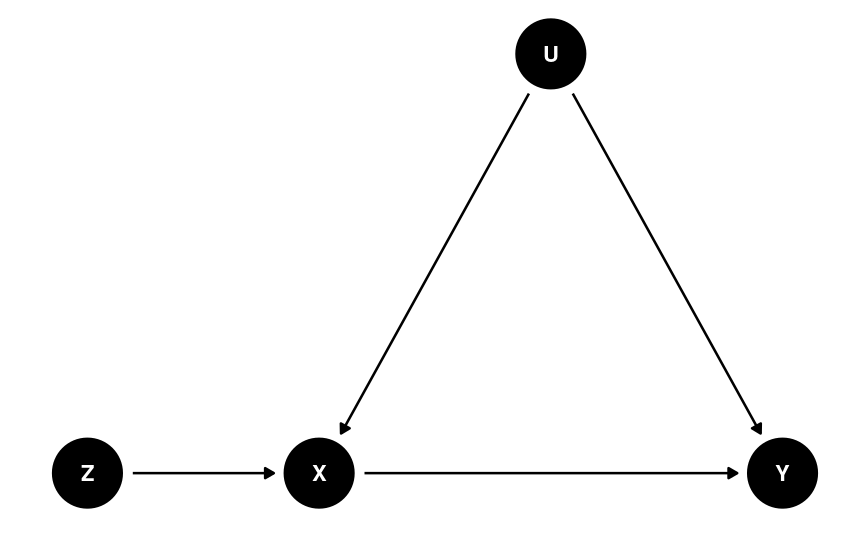
See more in the note
Remarks
- Causal inference requires causal assumptions
- You need a DAG
Remarks
- Causal inference requires causal assumptions
- You need a DAG
- Blindly adjusting for covariates does not give better results
- post-treatment bias, collider bias, etc
Remarks
- Causal inference requires causal assumptions
- You need a DAG
- Blindly adjusting for covariates does not give better results
- post-treatment bias, collider bias, etc
- Think carefully about what causal quantity is of interest
- E.g., direct, indirect, total
Remarks
- Causal inference requires causal assumptions
- You need a DAG
- Blindly adjusting for covariates does not give better results
- post-treatment bias, collider bias, etc
- Think carefully about what causal quantity is of interest
- E.g., direct, indirect, total
- Causal inferences are possible with both experimental and non-experimental data